Chemical reaction network theory
Chemical reaction network theory is a framework for modeling the evolution of chemical concentrations resulting from simultaneously occurring chemical reactions. A key feature of the theory is the relationship between the graphical structure of the reaction network and the resulting dynamics. A strong emphasis, consequently, is placed on results which hold regardless of the parameter values of the network, i.e. results which depend on the network structure alone.
The foundations of chemical reaction network theory were laid down in a series of seminal papers by Fritz Horn, Roy Jackson and Martin Feinberg in the early 1970's [1][2][3]. In these papers, the authors were primarily focused on developing conditions sufficient for uniqueness and stability of equilibrium concentrations, but their foundation has since between adapted to questions of multistability, injectivity, monotonicity, persistence, equivalence of mass-action systems, model reduction, oscillations, and applications. The models have also been adapted to the stochastic framework, reaction-diffusion equations, and kinetic schemes other than mass-action (e.g. Michaelis-Menten, Hill kinetics, etc.).
Chemical reaction networks
A chemical reaction network is given by sets of chemical species (or reactants) which react to form different sets of species. For example, consider the set of reactions corresponding to the Michaelis-Menten model for enzyme-facilitated transformation of a single substrate into a single product:
In this model S denotes the generic substrate, E denotes the enzyme facilitating the transfer, SE denotes the intermediate substrate-enzyme quantity, and P denotes the end product of the process. We define the species set of the network to be the collection of chemical species capable of undergoing basic chemical change. Another fundamental feature are the combined terms which appear on the left and right of each individual reaction (the net input and net output of a reaction). These terms are called complexes. If we count repeated complexes only once, we can define the complex set of the network as (since SE and S + E are repeated). Lastly, we define the reaction set to be the set of ordered pairs between elements of the complex set given by . The chemical reaction network is given by the triplet .
This formulation allows us to restructure the list of elementary reactions given above with each stoichiometrically distinct complex appearing only once. The resulting condensed graph is called the reaction graph of the network and is given by
In general, a chemical reaction network is defined by where is the species set, is the complex set, and is the reaction set.
See also:
The reaction graph
A chemical reaction network can be naturally represented as a directed graph G(V,E) where the set of vertices V is given by the complex set and the set of directed edges E is given by the reaction set . This reaction graph keeps track of the connections (through reactions) between the nodes of a graph (the stoichiometric distinct complexes). Many topics from graph theory are relevant to the study of the reaction graph of a chemical reaction network, and consequently to the study of the dynamics of the dynamical systems corresponding to reaction networks.
We can express any reaction network via a reaction graph by writing each stoichiometric distinct complex exactly once as a node in a graph, and representing the reactions as connections between these nodes. For example, we can reformulate the following list of reactions (left) as the reaction graph (right) by writing each stoichiometrically distinct complex only once
See also:
General kinetic framework
In order to translate a chemical reaction network into a dynamical framework, several assumptions need to be made. It is common to assume that the chemical species are in sufficient quantity to ignore stochastic effects (so that we may model the reaction continuously and deterministically over chemical concentrations) and that the medium where the reactions are occurring is well-mixed (so that there are no pockets of high concentrations of one species or another). (See the respective pages for information on stochastic and diffusive models.)
These assumptions lead to an ordinary differential equation model over the chemical concentrations. We let denote the vector of chemical concentrations corresponding to the n chemical species . In order to determine the dynamics, we need to determine the net stoichiometric change resulting from each reaction and the corresponding rate of the reaction. We will number the reactions from and define and to be the vectors of stoichiometric coefficients of the reactant and product complex of the reaction, respectively. We can then represent the dynamics of the chemical reaction network as
where corresponds to the rate of the reaction. This can be more compactly written in matrix form as
where the stoichiometric matrix contains the reaction vectors , as its columns and .
It is important to note that this formulation does not depend on specific assumptions on the rate functions of the individual reactions, and that those rates may be allowed to depend on time. They may be corresponded with a specific kinetic framework or be left general.
See also:
Mass action systems
The most commonly used form for the rate functions is that of mass action kinetics. Under this assumption, each reaction is assigned a positive rate constant , , from a rate constant set . The rate functions are then defined according to If we introduce the shorthand notation , we can write the system of ordinary differential equations governing the dynamics of a chemical reaction network under mass-action kinetics as
The mass action system associated with the chemical reaction network and the rate constant set is given by the quadruple .
In order to most clearly emphasize the connection between the reaction graph of a chemical reaction network and the behaviour of solutions under mass-action kinetics, it is common to reformulate the dynamical representation of mass-action systems by breaking the stoichiometric matrix and rate vector into forms which emphasize the connections between stoichiometrically distinct complexes. To this end, we reindex the complexes according to their stoichiometric distinctiveness, , , and define the complex matrix to be the matrix where the column is given by the stoichiometric vector corresponding to the complex and the mass-action vector to be the vector with entries for . We can write the mass-action system above as
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\vec{c}}{dt} = Y A_k \Psi(\vec{c}) }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_k \in \mathbb{R}_{\geq 0}^{m \times m}} is the kinetic or Kirchhoff matrix of the network.
Under the assumption of mass-action kinetics, chemical reaction networks give rise to a system of autonomous, polynomial ordinary differential equations (with no negative cross-effects). Despite this simple formulation, mass-action systems are known which exhibit varied and exotic behaviour, including stability, multistability, switching behaviour, finite escape time, oscillations, limit cycles, chaotic behaviour, and Hopf bifurcations. It is also worth noting that two mass-action systems with the same underlying reaction network Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} do not necessarily share the same qualitative behaviour (i.e. the dynamical behaviour of mass-action systems in general is rate-constant-dependent as well as network dependent).
See also:
- Detailed balanced systems
- Complex balanced systems
- Model reduction
- Polynomial ordinary differential equations
- Indexing
References
- ↑ R. Horn, R. Jackson, General mass action kinetics, Arch. Ration. Mech. Anal. 47 (1972) 81-116
- ↑ F. Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics, Arch. Ration. Mech. Anal., 49 (1972) 172-186
- ↑ M. Feinberg, Complex balancing in general kinetic systems, Arch. Ration. Mech. Anal., 49 (1972) 187-194
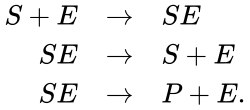
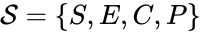 of the network to be the collection of chemical species capable of undergoing basic chemical change. Another fundamental feature are the combined terms which appear on the left and right of each individual reaction (the net input and net output of a reaction). These terms are called complexes. If we count repeated complexes only once, we can define the complex set of the network as
of the network to be the collection of chemical species capable of undergoing basic chemical change. Another fundamental feature are the combined terms which appear on the left and right of each individual reaction (the net input and net output of a reaction). These terms are called complexes. If we count repeated complexes only once, we can define the complex set of the network as 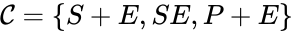 (since SE and S + E are repeated). Lastly, we define the reaction set to be the set of ordered pairs between elements of the complex set given by
(since SE and S + E are repeated). Lastly, we define the reaction set to be the set of ordered pairs between elements of the complex set given by 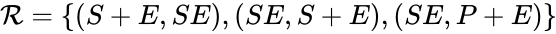 . The chemical reaction network is given by the triplet
. The chemical reaction network is given by the triplet 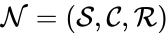 .
.
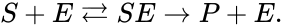
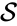 is the species set,
is the species set,  is the complex set, and
is the complex set, and 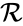 is the reaction set.
is the reaction set.
![{\displaystyle {\begin{array}{rclccc}{\mathcal {A}}_{1}&\;\longrightarrow \;&{\mathcal {A}}_{2}&{\mathcal {A}}_{1}\;\longrightarrow \;{\mathcal {A}}_{2}\\[0.1cm]{\mathcal {A}}_{2}&\;\longrightarrow \;&{\mathcal {A}}_{3}+{\mathcal {A}}_{4}\;\;\;\;\;\;\;\;\;\;\Longrightarrow \;\;\;\;\;\;\;\;\;\;&\nwarrow \;\;\;\;\;\swarrow \\[0.1cm]{\mathcal {A}}_{3}+{\mathcal {A}}_{4}&\;\longrightarrow \;&{\mathcal {A}}_{1}&{\mathcal {A}}_{3}+{\mathcal {A}}_{4}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/62a8f6f066cf28bc31e01057282ef1c5644a2f6f)
![{\displaystyle {\vec {c}}=[c_{1},c_{2},\ldots ,c_{n}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/2b58baf74316d120e0f51644be20d8a200ef18d0) denote the vector of chemical concentrations corresponding to the n chemical species
denote the vector of chemical concentrations corresponding to the n chemical species  . In order to determine the dynamics, we need to determine the net stoichiometric change resulting from each reaction and the corresponding rate of the reaction. We will number the reactions from
. In order to determine the dynamics, we need to determine the net stoichiometric change resulting from each reaction and the corresponding rate of the reaction. We will number the reactions from  and define
and define 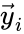 and
and 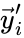 to be the vectors of stoichiometric coefficients of the reactant and product complex of the
to be the vectors of stoichiometric coefficients of the reactant and product complex of the 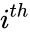 reaction, respectively. We can then represent the dynamics of the chemical reaction network
reaction, respectively. We can then represent the dynamics of the chemical reaction network 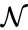 as
as

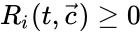 corresponds to the rate of the
corresponds to the rate of the 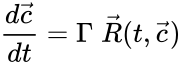
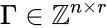 contains the reaction vectors
contains the reaction vectors 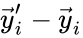 ,
, 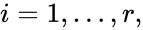 as its columns and
as its columns and ![{\displaystyle {\vec {R}}(t,{\vec {c}})=[R_{1}(t,{\vec {c}}),\ldots ,R_{r}(t,{\vec {c}})]^{T}\in \mathbb {R} _{\geq 0}^{r}}](https://wikimedia.org/api/rest_v1/media/math/render/png/5a6d712f82e4862d8f4c94d93e2f94d61d34180c) .
.
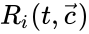 of the individual reactions, and that those rates may be allowed to depend on time. They may be corresponded with a specific kinetic framework or be left general.
of the individual reactions, and that those rates may be allowed to depend on time. They may be corresponded with a specific kinetic framework or be left general.
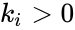 ,
, 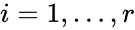 , from a rate constant set
, from a rate constant set 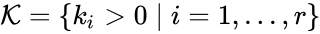 . The rate functions are then defined according to
. The rate functions are then defined according to  If we introduce the shorthand notation
If we introduce the shorthand notation 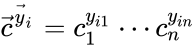 , we can write the system of ordinary differential equations governing the dynamics of a chemical reaction network under mass-action kinetics as
, we can write the system of ordinary differential equations governing the dynamics of a chemical reaction network under mass-action kinetics as
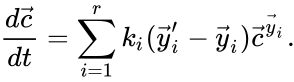
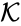 is given by the quadruple
is given by the quadruple 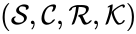 .
.
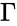 and rate vector
and rate vector 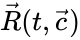 into forms which emphasize the connections between stoichiometrically distinct complexes. To this end, we reindex the complexes according to their stoichiometric distinctiveness,
into forms which emphasize the connections between stoichiometrically distinct complexes. To this end, we reindex the complexes according to their stoichiometric distinctiveness, 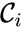 ,
, 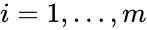 , and define the
, and define the  to be the matrix where the
to be the matrix where the 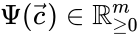 to be the vector with entries
to be the vector with entries 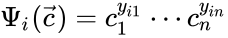 for
for