Dynamical equivalence
Two mass action systems and are said to be dynamically equivalent if the differential equations produced under the assumption of mass action kinetics are identical. Two mass action systems which given rise to the same differential equation set are sometimes said to be alternative realizations of the same kinetics.
It has been known since at least the early 1970s that two mass action systems with distinct rate constants and network structure can given rise to the same dynamics. Frederick J. Krambeck considered such systems arising from detailed balancing[1] (which he called non-uniqueness of parameters) and Fritz Horn and Roy Jackson considered it for a class of weakly reversible networks[2] (which they called macro-equivalence). A thorough study of the capacity of networks to be dynamically equivalence was conducted by Gheorghe Craciun and Casian Pantea[3] (they called the phenomenon counfoundability of mass action systems).
Recent research on dynamical equivalence of mass action systems has been focused on two primary problems:
- Identifiability of network structure - The reality that mass action systems with different underlying network structure may give rise to the same dynamics provides a limitation for the inverse problem of chemical kinetics. Specifically, even if we have perfect knowledge about the dynamics of a chemical kinetic system, we may not be able to uniquely determine the network structure which gave rise to the dynamics. This is a significant concern and limitation in application as we typically only have measurable information at the end of a process and must infer the network structure. Exploring the limits of permissible networks with dynamically equivalent kinetics has consequently been a focus in chemical reaction network theory[4][3][5][6].
- Correspondence of dynamics - It is possible for two mass action systems to be dynamically equivalent even when only one of them has a typically desirable feature about either their dynamics (e.g. detailed balancing, complex balancing, etc.) or their underlying network structure (e.g. reversibility, weak reversibility, low deficiency, etc.). In these cases, the dynamical property guaranteed by the desirable systems applies to the system which does not have the property. In other words, the scope of mass action systems with the desirable property is expanded. Determining conditions which expand the scope of applicability of classical results (e.g. deficiency theory, detailed balancing, complex balancing, etc.) has been a focus of research [7][8] and in recent years specifically has taken a turn toward computational methods[9][10][11][12][13][14][15]
Identifiability of chemical reaction networks
Correspondence of dynamics
It is possible for two mass action systems and to exhibit qualitative identical behavior despite difference in network structure, and even subtle differences in the underlying differential equations governing the system. It is particularly noteworthy that this may hold despite significant differences in the connectedness and reversibility of the reaction graphs of the chemical reaction networks underlying the systems. That is to say, one of the networks underlying the mass action systems involved may have a desirable structural property (weak reversibility, endotacticity, single linkage class, etc.) while the other may not.
The realization that two systems exhibit the same dynamics can be a powerful analysis tool when results are known which guarantee one of the systems has known dynamic properties (e.g. locally stable dynamics, multistationarity, persistence, etc.). These tools can therefore be used to expand the scope of existing theory to systems for which the underlying network would not otherwise guarantee such behavior.
Dynamical equivalence
It is possible for two mass action systems and to give rise to identical systems systems of differential equations despite differences in the complex set , the reaction set , and/or the kinetic rate constants .
For example, consider the four-complex network considered by Fritz Horn and Roy Jackson[2]:
The network is weakly reversible but has a deficiency of two so that the mass action system does not fall within the scope of the Deficiency Zero Theorem. The conditions of the General Deficiency Theorem guarantee that the mass action system is complex balanced if and only if . Outside of this value, deficiency theory is silent.
Consider, however, the reaction vector associated with the reaction from the complex . For , we can rescale and split the mass action term corresponding to this reaction according to
In other words, the reaction can be split into two, one linking to and one linking to . Performing the same analysis on the reaction from yields the dynamically equivalent system
for which the equilibrium concentration is always a complex balanced equilibrium concentration. In other words, we can show that the original network behaves like a complex balanced system for all by rewriting the system in a way that it corresponds to a system with different underlying network structure.
Consider similarly splitting the reaction from . For we have
In other words, we can split the reaction into two, one linking to and one linking to . Performing the analogous procedure on the reaction originating from gives us the dynamically equivalent network
where the unlabelled reactions have rate constant . The equilibrium concentration is always a complex balanced equilibrium concentration for this system. Piecing this together with the previous decomposition, we have that by restructuring the mass action equations, we can show that the network behaves like a complex balanced mass action system (that is to say, exhibits locally stable dynamics) for all despite being only complex balanced for the value . This is a significant improvement over the results guaranteed by consider the original formulation of the network, although it does fall short of capturing the whole range of parameter values capable of producing locally stable dynamics, which is known to be .
Linear conjugacy
Two mass action systems and for which the flows of the corresponding differential equations are related by a non-trivial linear transformation are said to be linearly conjugate. Formally, suppose that the mass action system has flow and the mass action system corresponding to has flow . The two systems are said to be linearly conjugate to one another if there exists a linear mapping such that for all .
Linearly conjugacy was introduced by Matthew Johnston and David Siegel in [16] as a generalization of dynamical equivalence. Dynamical equivalence can be thought of as a trivial linear conjugacy; that is to say, a linearly conjugate relationship where the conjugate map is the identity. Linear conjugacy is also related to the concept of lumping.
For example, consider the chemical reaction networks[15]
Under the assumption of mass action kinetics, these networks give rise to the following governing set of ordinary differential equations
It is clear that these networks are not dynamically equivalent since they do not have an identical set of governing differential equations. For any set of rate constants, however, trajectories for the system corresponding to can be related to that of by the linear relationship . Since is a reversible network with zero deficiency, it follows by the Deficiency zero theorem that exhibits locally stable dynamics. It follows by the nature of the conjugacy mapping that exhibits the same qualitative dynamics.
It is known that the linear mapping may preserve mass action kinetics if and only if it has precisely one nonzero entry in each row and column, and that entry is positive (Lemma 3.1 [16]). In other words, the mapping may only permute and rescale the species. It is also common to restrict permutation so that is a diagonal matrix with positive weighted entries on its diagonal.
Computational approaches
References
- ↑ Frederick J. Krambeck, The mathematical structure of chemical kinetics in homogeneous single-phase systems, Arch. Rational Mech. Anal., 38:317--347, 1970
- ↑ 2.0 2.1 Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:187--194, 1972
- ↑ 3.0 3.1 Gheorghe Craciun and Casian Pantea, Identifiability of chemical reaction networks, J. Math Chem., 44(1):244--259, 2008
- ↑ V. Hars and Janos Toth, On the inverse problem of reaction kinetics, Coll. Math. Soc. J. Bolyai, 30:363--379, 1981
- ↑ Gheorghe Craciun, Casian Pantea, and Grzegorz Rempala, Algebraic methods for inferring biochemical networks: a maximum likelihood approach, Compute. Biol. Chem., 33(5):361--367, 2009
- ↑ Gheorghe Craciun, Jaejik Kim, Casian Pantea, and Grzegorz A. Rempala, Statistical Model for Biochemical Networks Inference, to appear in Communications in Statistics: Simulation and Computation, 2012
- ↑ Einstein D. Averbukh, Some equivalent kinetic functions of macrodynamic equations, Automation and Remote Control, 55(11):1694--1698, 1994
- ↑ Einstein D. Averbukh, Complex balanced kinetic functions in inverse problems of chemical kinetics, Automation and Remote Control, 55(12):1723--1732, 1994
- ↑ Gabor Szederkenyi, Computing sparse and dense realizations of reaction kinetic systems, J. Math. Chem., 47:551--568, 2010
- ↑ Gabor Szederkenyi and Katalin Hangos, Finding complex balanced and detailed balanced realizations of chemical reaction networks, J. Math. Chem., 49:1163--1179, 2011
- ↑ Gabor Szederkenyi, Katalin Hangos, and Tamas Peni, Maximal and minimal realizations of chemical kinetics systems: computation and properties.MATCH Commun. Math. Comput. Chem., 65:309--332, 2011
- ↑ Gabor Szederkenyi, Katalin Hangos, and Zsolt Tuza, Finding weakly reversible realizations of chemical reaction networks using optimization. MATCH Commun. Math. Comput. Chem., 67:193--212, 2012
- ↑ Matthew D. Johnston, David Siegel, and Gabor Szederkenyi, A linear programming approach to weak reversibility and linear conjugacy of chemical reaction networks, J. Math. Chem., 50(1):274--288, 2012
- ↑ Matthew D. Johnston, David Siegel, and Gabor Szederkenyi, Dynamical equivalence and linear conjugacy of chemical reaction networks: New results and methods, to appear in MATCH Commun. Math. Comput. Chem., 2012
- ↑ 15.0 15.1 Matthew D. Johnston, David Siegel, and Gabor Szederkenyi, Computing weakly reversible linearly conjugate chemical reaction networks with minimal deficiency, to appear in Math. Biosci., 2012
- ↑ 16.0 16.1 Matthew D. Johnston and David Siegel, Linear conjugacy of chemical reaction networks, J. Math. Chem., 49(7):1263--1282, 2011.
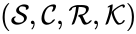 and
and 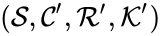 are said to be dynamically equivalent if the
are said to be dynamically equivalent if the  , the
, the 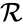 , and/or the
, and/or the 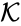 .
.
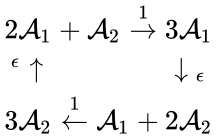
 . Outside of this value, deficiency theory is silent.
. Outside of this value, deficiency theory is silent.
 . For
. For  , we can rescale and split the
, we can rescale and split the ![{\displaystyle \left[{\begin{array}{c}1\\-1\end{array}}\right]c_{1}^{2}c_{2}=\left({\frac {1+2\epsilon }{3}}\left[{\begin{array}{c}1\\-1\end{array}}\right]+{\frac {\epsilon -1}{3}}\left[{\begin{array}{c}-2\\2\end{array}}\right]\right)c_{1}^{2}c_{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/png/b8a5e3a743e6951aca8a41e7efdddde72cd82535)
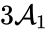 and one linking to
and one linking to 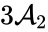 . Performing the same analysis on the reaction from
. Performing the same analysis on the reaction from 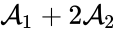 yields the dynamically equivalent system
yields the dynamically equivalent system
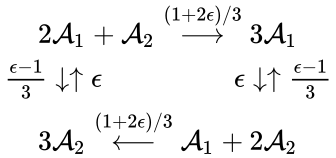
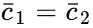 is always a complex balanced equilibrium concentration. In other words, we can show that the original network behaves like a complex balanced system for all
is always a complex balanced equilibrium concentration. In other words, we can show that the original network behaves like a complex balanced system for all 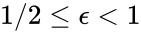 we have
we have
![{\displaystyle \epsilon \left[{\begin{array}{c}-2\\2\end{array}}\right]c_{1}^{3}=\left(\left(2\epsilon -1\right)\left[{\begin{array}{c}-2\\2\end{array}}\right]+\left(2-2\epsilon \right)\left[{\begin{array}{c}-1\\1\end{array}}\right]\right)c_{1}^{3}.}](https://wikimedia.org/api/rest_v1/media/math/render/png/c943dac1cb8a979ed64d7455fe96fa36df0b1ecf)
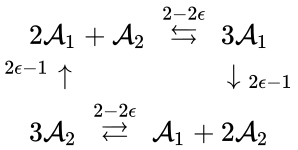
 . The equilibrium concentration
. The equilibrium concentration 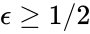 despite being only complex balanced for the value
despite being only complex balanced for the value 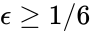 .
.
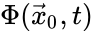 and the mass action system corresponding to
and the mass action system corresponding to 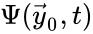 . The two systems are said to be linearly conjugate to one another if there exists a linear mapping
. The two systems are said to be linearly conjugate to one another if there exists a linear mapping 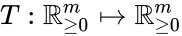 such that
such that 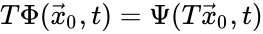 for all
for all  .
.
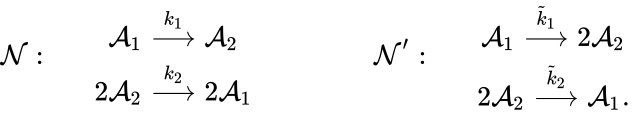
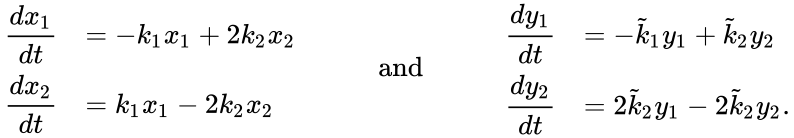
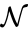 can be related to that of
can be related to that of 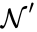 by the linear relationship
by the linear relationship 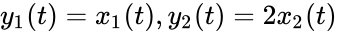 . Since
. Since  may preserve
may preserve