Locally stable dynamics
A chemical reaction network associated with some kinetic scheme is said to have locally stable dynamics if there exists within each positive stoichiometric compatibility class exactly one equilibrium concentration , and if this equilibrium concentration is locally asymptotically stable relative to its compatibility class. That is to say, trajectories within the invariant space as and close enough to it converge asymptotically to .
Many kinetic systems within chemical reaction network theory are known to exhibit locally stable dynamics, in particular, detailed[1] and complex balanced[2] mass action systems. It precludes such exotic behavior as multistability.
Locally stable dynamics can be naturally extended globally stable dynamics when the unique equilibrium concentration in each compatibility class is known to an attractor for the entire set . Extending locally stable dynamics to globally stable dynamics for complex balanced mass action systems is the content of the Global Attractor Conjecture, one of the longest-standing and best known conjectures in chemical reaction network theory [3][4].
The term "locally stable dynamics" first appeared in the papers of David Siegel and Matthew D. Johnston in an attempt to standardize and simplify the terminology for what is a recurrent concept throughout chemical reaction network theory [5][6]. It is not otherwise widely used.
References
- ↑ Aizik I. Vol'pert and Sergei I. Hudjaev, Analysis in Classes of Discontinuous Functions and Equations of Mathematical Physics, Martinus Nijhoff Publishers, Dordrecht, Netherlands, 1985
- ↑ Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:81--116, 1972
- ↑ Gheorghe Craciun, Alicia Dickenstein, Anne Shiu, and Bernd Sturmfels, Toric dynamical systems, J. Symbolic Comput., 44(11):1551--1565, 2009
- ↑ David Anderson, A proof of the global attractor conjecture in the single linkage class case, SIAM J. Appl. Math., 71(4):1487--1508, 2011
- ↑ Matthew D. Johnston and David Siegel, Linear conjugacy of chemical reaction networks, J. Math. Chem., 49(7):1263--1282, 2011
- ↑ David Siegel and Matthew D. Johnston, A stratum approach to global stability of complex balanced systems, Dyn. Syst., 26(2):125--146, 2011
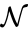 associated with some
associated with some 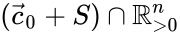 exactly one
exactly one 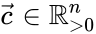 , and if this equilibrium concentration is locally asymptotically stable relative to its compatibility class. That is to say, trajectories within the invariant space as
, and if this equilibrium concentration is locally asymptotically stable relative to its compatibility class. That is to say, trajectories within the invariant space as 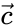 and close enough to it converge asymptotically to
and close enough to it converge asymptotically to