K-variable kinetics
Jump to navigation
Jump to search
A chemical reaction network is said to be endowed with k-variable kinetics if the kinetic vector has entries of the form
where is the stoichiometric vector for the reactant complex of the reaction and , for , for .
K-variable kinetics is a generalization of mass action kinetics which allows the rate of each reaction to vary within a compact region over time. The terminology "k-variable kinetics" was introduced by Gheorghe Craciun, Casian Pantea and Fedor Nazarov[1] and has been further studied by Casian Pantea[2] and David Anderson[3], who called the kinetics "bounded mass action kinetics".
References
- ↑ Gheorghe Craciun, Casian Pantea, and Fedor Nazarov, Persistence and permanence of mass-action and power-law dynamical systems, to appear SIAM J. Appl. Math., 2012
- ↑ Casian Pantea, On the persistence and global stability of mass-action systems, SIAM J. Math. Anal., 44(3), 2012
- ↑ David Anderson, A proof of the global attractor conjecture in the single linkage class case, SIAM J. Appl. Math., 71(4):1487--1508, 2011
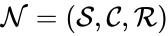 is said to be endowed with k-variable kinetics if the
is said to be endowed with k-variable kinetics if the 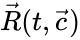 has entries of the form
has entries of the form

![{\displaystyle {\vec {y}}_{i}=[y_{1i},\ldots ,y_{ni}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/d8d90beba348232f8c49849c434d3cf255defb48) is the
is the 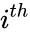 reaction and
reaction and 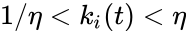 , for
, for 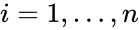 , for
, for  .
.