Persistence
Jump to navigation
Jump to search
A chemical reaction network endowed with some kinetic scheme is said to be persistent if initial present species are not allowed to approach extinction, either directly or asymptotically (i.e. as a limit of subsequences). That is to say, a network is persistent if for implies
for . For systems which are known to have bounded trajectories, this is equivalent to the condition where is the omega-limit set of the trajectory with initial condition .
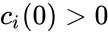 for
for 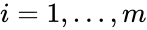 implies
implies
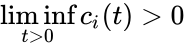
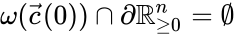 where
where 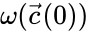 is the omega-limit set of the trajectory with initial condition
is the omega-limit set of the trajectory with initial condition 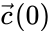 .
.