Mass action kinetics
Mass action kinetics is a kinetic scheme for chemical reaction networks which says that the rate of a chemical reaction is proportional to the product of the concentrations of the reacting chemical species. It was first formulated by Cato Maximilian Guldberg and Peter Waage in the 1860's [1]. It remains one of the most common kinetic assumptions used by chemists, biologists, and mathematicians.
Deterministic modeling
In the ordinary differential equation modeling of chemical reaction networks, the assumption of mass-action kinetics produces polynomial vector fields. For example, consider the reaction given by
If we let and denote the concentrations of A and B respectively, then the reaction occurs at a rate proportional to . That is to say, we have
where is the (fixed) proportionality rate (or rate constant) associated with the reaction. Since each instance of the reaction produces a net decrease of one molecule of A and B each, and an increase of one molecule of C, we can model the reaction as
Stochastic modeling
References
- ↑ C.M. Guldberg and P. Waage, Studies Concerning Affinity, C. M. Forhandlinger: Videnskabs-Selskabet i Christiana (1864), 35
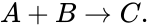
![{\displaystyle [A]}](https://wikimedia.org/api/rest_v1/media/math/render/png/79eaa334597b1861f1b08ca0c8fecb3858ebcb12) and
and ![{\displaystyle [B]}](https://wikimedia.org/api/rest_v1/media/math/render/png/6e6c6caf9d188e4a608dfdac98bbcd140a9ea106) denote the concentrations of A and B respectively, then the reaction occurs at a rate proportional to
denote the concentrations of A and B respectively, then the reaction occurs at a rate proportional to ![{\displaystyle [A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/png/d66331a8300fdf8d0be4c6882c5574b4c173e6f0) . That is to say, we have
. That is to say, we have
![{\displaystyle [{\mbox{rate of reaction}}]\propto [A][B]\;\;\;\;\;{\mbox{ or }}\;\;\;\;\;[{\mbox{rate of reaction}}]=k[A][B].}](https://wikimedia.org/api/rest_v1/media/math/render/png/50d2a42152de3cc88dfd7f36480621751edcfb7f)
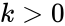 is the (fixed) proportionality rate (or rate constant) associated with the reaction. Since each instance of the reaction produces a net decrease of one molecule of A and B each, and an increase of one molecule of C, we can model the reaction as
is the (fixed) proportionality rate (or rate constant) associated with the reaction. Since each instance of the reaction produces a net decrease of one molecule of A and B each, and an increase of one molecule of C, we can model the reaction as
![{\displaystyle {\begin{array}{rcl}{\frac {d[A]}{dt}}&=&-k[A][B]\\{\frac {d[B]}{dt}}&=&-k[A][B]\\{\frac {d[C]}{dt}}&=&k[A][B].\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/f9633f278fb51bc9f0f12e2cb05277774ccbdded)