Chemical reaction networks
A chemical reaction network is given by the triplet where is the species set, is the complex set, and is the reaction set.
Chemical reaction networks are the central objects of study in the Chemical Reaction Network Theory (CRNT) initiated and developed by Fritz Horn, Roy Jackson, and Martin Feinberg in the 1970s [1][2][3]. Chemical reaction networks are most commonly associated with mass action kinetics, which assigns to each reaction in the reaction set a positive proportionality rate (i.e. rate constant). This gives rise to the mass action system where denotes the rate constant set; however, other kinetic schemes are also common (e.g. Michaelis-Menten kinetics, k-variable mass action kinetics, Hill kinetics, etc.).
A primary focus in chemical reaction network theory is on the relationship between the structure of the reaction graph of a network and the qualitative dynamical behavior of the corresponding kinetic systems. This parameter-free approach makes the theory of particular interest to biochemistry where there is a large number of parameters, many of which may not be known with great precision.
Species
The species set of a chemical reaction network is defined as where for are the individual chemical species capable of undergoing chemical change. In most applications, the concentrations or amounts of the individual species are the dynamical quantities of primary interest. That is to say, when constructing our dynamical model, we are generally interested in the time-evolution of these quantities. The concentration of the species is denoted by .
Depending on the specific application in question, the individual species may correspond to quantities with well-defined chemical structure, or they may not. For example, in the overall equation for the electrolysis of water given by
we have the chemical species , , and . We are interested in both the composition of the individual chemical species and the notion of conservation of those components, that is to say, the chemical requirement that equal numbers of hydrogen and oxygen appear on the left-hand and right-hand side of the equations. Consider instead the Michaelis-Menten mechanism
we have the chemical species (substrate), (enzyme), (substrate-enzyme complex), and (product). The mechanism is general enough, and the individual species involved complicated enough, that we are no longer interested in the specific chemical composition of the species. We notice we are still, however, interested in the notion of conservation of chemical species. For example, everything that composed the substrate is found in equal amounts in every step of the mechanism (i.e. in , , and ). That is not always the case. For example in continuous flow stirred-tank reactions (CFSTR), where we imagine an inflow and outflow stream to a tank where a chemical reaction (or series of reactions) is occurring, it is typical to add reactions of the form
where the forward reaction corresponds to inflow and the backward reaction corresponds to outflow. These reactions do not conserve any chemical component of the species . It is also common to remove chemical conservation in reactions involve a species which is of limitless supply, for example, reactions which occur at small concentrations with water where water in the medium of the reaction. For example, we could represent a reaction
if we are justified in assuming the occurrence of the reaction would not change the effective concentration of .
It is also worth noting that the notion of species may be made more general than chemical species. The Lotka-Volterra model for predator-prey modeling, for instance, may be modeled with the reaction network
We let correspond to the prey and correspond to the predator and imagine the first "reaction" models the predator eating the prey, the second models the prey reproducing, and the third models the death of the predator.
Complexes
The complex set of a chemical reaction network is defined as where for are the net inputs or outputs of an individual reaction. The non-negative integer terms are called stoichiometric coefficients and may be indexed according to either the reactions or the stoichiometrically distinct complexes, depending on the application. In either case, the stoichiometric coefficients represent the multiplicity of the chemical species in the complexes.
Every reaction in a chemical reaction network can be represented in the form for some stoichiometrically distinct complexes . That is to say, they are the vertices (or nodes) appearing at the tail or head of a reaction arrow in the reaction graph of a network. In this setting, the stoichiometrically distinct complexes are allowed appear at the tail or head of multiple reactions if necessary. For example, in the Michaelis-Menten example above, we can set , , and and represent the network as
It is also common[4][5], although a slight abuse of notation, to equate the stoichiometric vectors , , with the complexes (i.e. set , , and ) and represent the network as
It is sometimes convenient to separate complexes into source complexes (those which appear on the reactant side of a reaction) and product complexes (those which appear on the reactant side of a reaction). The set of source complexes is denoted . The complex with all stoichiometric coefficients , is called the zero complex and is denoted or .
Reactions
The reaction set is defined as .
Requirements
It is customary to assume that a chemical reaction network does not admit any specie which does not appear in any reaction (i.e. all species appear in the network) or any complex which does not appear in any reaction (i.e. all complexes appear in the network). It is also customary to exclude reactions of the form (i.e. there are no self-reactions).
References
- ↑ Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:81--116, 1972
- ↑ Fritz Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal., 49:172--186, 1972
- ↑ Martin Feinberg, Complex balancing in general kinetic systems, Arch. Ration. Mech. Anal., 49:187--194, 1972
- ↑ Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: II. multiple steady states for networks of deficiency one, Chem. Eng. Sci., 43(1):1--25, 1988
- ↑ David Anderson, A proof of the global attractor conjecture in the single linkage class case, SIAM J. Appl. Math., 71(4):1487--1508, 2011
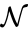 is given by the triplet
is given by the triplet 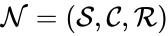 where
where 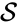 is the species set,
is the species set,  is the complex set, and
is the complex set, and 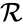 is the reaction set.
is the reaction set.
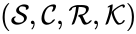 where
where 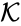 denotes the rate constant set; however, other kinetic schemes are also common (e.g.
denotes the rate constant set; however, other kinetic schemes are also common (e.g. 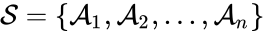 where
where  for
for 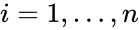 are the individual chemical species capable of undergoing chemical change. In most applications, the concentrations or amounts of the individual species are the dynamical quantities of primary interest. That is to say, when constructing our dynamical model, we are generally interested in the time-evolution of these quantities. The concentration of the
are the individual chemical species capable of undergoing chemical change. In most applications, the concentrations or amounts of the individual species are the dynamical quantities of primary interest. That is to say, when constructing our dynamical model, we are generally interested in the time-evolution of these quantities. The concentration of the 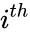 species
species ![{\displaystyle c_{i}=[{\mathcal {A}}_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/87fc54a7c0195b3245eb536e4e2f00686f8c228a) .
.
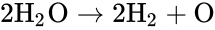
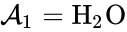 ,
, 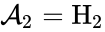 , and
, and 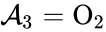 . We are interested in both the composition of the individual chemical species and the notion of conservation of those components, that is to say, the chemical requirement that equal numbers of hydrogen and oxygen appear on the left-hand and right-hand side of the equations. Consider instead the
. We are interested in both the composition of the individual chemical species and the notion of conservation of those components, that is to say, the chemical requirement that equal numbers of hydrogen and oxygen appear on the left-hand and right-hand side of the equations. Consider instead the 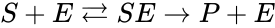
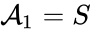 (substrate),
(substrate), 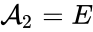 (enzyme),
(enzyme), 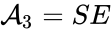 (substrate-enzyme complex), and
(substrate-enzyme complex), and 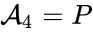 (product). The mechanism is general enough, and the individual species involved complicated enough, that we are no longer interested in the specific chemical composition of the species. We notice we are still, however, interested in the notion of
(product). The mechanism is general enough, and the individual species involved complicated enough, that we are no longer interested in the specific chemical composition of the species. We notice we are still, however, interested in the notion of 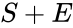 ,
, 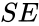 , and
, and 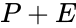 ). That is not always the case. For example in
). That is not always the case. For example in 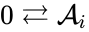

 .
.
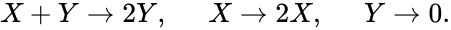
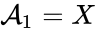 correspond to the prey and
correspond to the prey and 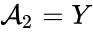 correspond to the predator and imagine the first "reaction" models the predator eating the prey, the second models the prey reproducing, and the third models the death of the predator.
correspond to the predator and imagine the first "reaction" models the predator eating the prey, the second models the prey reproducing, and the third models the death of the predator.
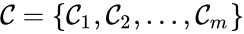 where
where 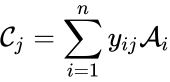 for
for 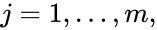 are the net inputs or outputs of an individual reaction. The non-negative integer terms
are the net inputs or outputs of an individual reaction. The non-negative integer terms 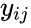 are called
are called 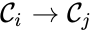 for some stoichiometrically distinct complexes
for some stoichiometrically distinct complexes 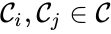 . That is to say, they are the vertices (or nodes) appearing at the tail or head of a reaction arrow in the
. That is to say, they are the vertices (or nodes) appearing at the tail or head of a reaction arrow in the  ,
, 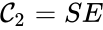 , and
, and 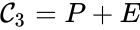 and represent the network as
and represent the network as
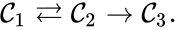
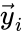 ,
, 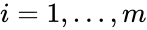 , with the complexes (i.e. set
, with the complexes (i.e. set ![{\displaystyle {\vec {y}}_{1}=[1,1,0,0]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/be09d6c99da86f0504a2cf8fec7cb0bcb8b42313) ,
, ![{\displaystyle {\vec {y}}_{2}=[0,0,1,0]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/d2ee14967dbc113d360a410734edddf219d6b2d4) , and
, and ![{\displaystyle {\vec {y}}_{3}=[0,1,0,1]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/82cf0fc89947144ff98e64ebe2c0e0d27b64d77b) ) and represent the network as
) and represent the network as
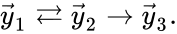
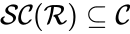 . The complex with all stoichiometric coefficients
. The complex with all stoichiometric coefficients 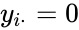 ,
, 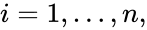 is called the zero complex and is denoted
is called the zero complex and is denoted 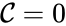 or
or 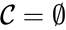 .
.
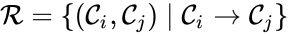 .
.
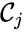 which does not appear in any reaction (i.e. all complexes appear in the network). It is also customary to exclude reactions of the form
which does not appear in any reaction (i.e. all complexes appear in the network). It is also customary to exclude reactions of the form 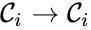 (i.e. there are no self-reactions).
(i.e. there are no self-reactions).