Detailed balanced mass action systems
A detailed balanced equilibrium concentration of a mass action system is a point which satisfies
for all . Using the short-hand notation we can rewrite this as for all . A mass-action system is said to be detailed balanced if every equilibrium concentration permitted by the system is a detailed balanced equilibrium concentration.
Detailed balancing guarantees that every elementary step in the reaction mechanism is balanced by a reverse elementary step at equilibrium. Every chemical reaction network which permits a detailed balanced mass action system is reversible (Theorem 2A[1]).
Matrix formulation
Detailed balancing at equilibrium can be alternatively characterized by the matrix expression
where is the mass action vector, is the kinetic or Kirchhoff matrix, and where is the matrix with the elements along the diagonal and zeroes elsewhere.
Properties of detailed balanced mass action systems
References
- ↑ Fritz Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal., 49:172--186, 1972
![{\displaystyle {\vec {a}}=[a_{1},a_{2},\ldots ,a_{n}]^{T}\in \mathbb {R} _{>0}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/png/15acae80a6a527776a408e6582ece7bffcd07c78) is a point which satisfies
is a point which satisfies
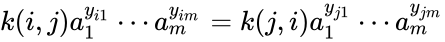
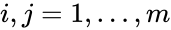 . Using the short-hand notation
. Using the short-hand notation 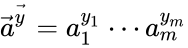 we can rewrite this as
we can rewrite this as 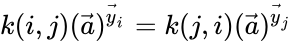 for all
for all 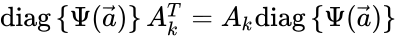
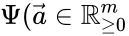 is the
is the  is the
is the 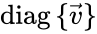 where
where ![{\displaystyle {\vec {v}}=[v_{1},v_{2},\ldots ,v_{m}]^{T}\in \mathbb {R} ^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/png/5740fde495a637272f086ea6abfb247c01e87a76) is the
is the  matrix with the elements
matrix with the elements 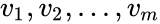 along the diagonal and zeroes elsewhere.
along the diagonal and zeroes elsewhere.