Monotone systems theory applied to reaction networks
Jump to navigation
Jump to search
Monotone systems theory was originally pioneered by Morris Hirsch in the 1980s [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14]. The theory was further developed by a number of other mathematicians, including Stephen Smale and Hal Smith.
A dynamical system is monotone if its mapping is order preserving, i.e. given any two initial states that are ordered with respect to some partial order, , their images are also ordered: .
References
- ↑ M. W. Hirsch, Convergence in ordinary and partial differential equations, Notes for Colloquium Lectures at University of Toronto, August 23-26, 1982. Providence, R. I. : Amer. Math. Soc. (1982).
- ↑ M. W. Hirsch, Systems of differential equations which are competitive or cooperative. I: limit sets. SIAM J. Appl. Math. 13 (1982), 167-179.
- ↑ M. W. Hirsch, Differential equations and convergence almost everywhere in strongly monotone semiflows, Contemp. Math. 17 (1983), 267-285.
- ↑ M. W. Hirsch, The dynamical systems approach to differential equations. Bull. A. M. S. 11 (1984), 1-64.
- ↑ M. W. Hirsch, Systems of differential equations which are competitive or cooperative. II: convergence almost everywhere. SIAM J. Math. Anal. 16 (1985), 423-439.
- ↑ M. W. Hirsch, Attractors for discrete-time monotone dynamical systems in strongly ordered spaces, Geometry and Topology, Lecture Notes in Mathematics vol. 1167, J. Alexander and J. Harer eds., 141-153. New York: Springer-Verlag (1985).
- ↑ M. W. Hirsch, Systems of differential equations which are competitive or cooperative. III: Competing species. Nonlinearity 1 (1988), 51-71.
- ↑ M. W. Hirsch, Stability and Convergence in Strongly Monotone dynamical systems, J. reine angew. Math. 383 (1988), 1-53.
- ↑ M. W. Hirsch, Convergent activation dynamics in continuous time neural networks, Neural Networks 2 (1989)
- ↑ M. W. Hirsch, Systems of differential equations that are competitive or cooperative. IV: Structural stability in three dimensional systems. SIAM J. Math. Anal. 21 (1990), 1225-1234.
- ↑ M. W. Hirsch, (1989) Systems of differential equations that are competitive or cooperative. V: Convergence in 3-dimensional systems. J. Diff. Eqns. 80 (1989), 94-106.
- ↑ M. W. Hirsch, Systems of differential equations that are competitive or cooperative. VI: A local closing lemma for 3-dimensional systems. Ergod. Th. Dynamical Sys. 11 (1991), 443-454.
- ↑ M. W. Hirsch, Fixed points of monotone maps, J. Differential Equations 123(1995), 171-179.
- ↑ M. W. Hirsch, Chain transitive sets for smooth strongly monotone dynamical systems, Diff. Eqns. and Dynamical Systems 5 (1999) 529-543.
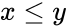 , their images are also ordered:
, their images are also ordered: 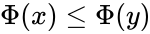 .
.
 closing lemma for 3-dimensional systems. Ergod. Th. Dynamical Sys. 11 (1991), 443-454.
closing lemma for 3-dimensional systems. Ergod. Th. Dynamical Sys. 11 (1991), 443-454.