Hill kinetics
The Hill equation is an equation used in biochemical characterization. In biochemistry, the binding of a ligand to a macromolecule is often enhanced if there are already other ligands present on the same macromolecule (this is known as cooperative binding). The Hill coefficient, named for Archibald Vivian Hill, provides a way to quantify this effect.
It describes the fraction of the macromolecule saturated by ligand as a function of the ligand concentration; it is used in determining the degree of cooperativeness of the ligand binding to the enzyme or receptor. It was originally formulated by Archibald Hill in 1910 to describe the sigmoidal O2 binding curve of haemoglobin.[1]
A coefficient of 1 indicates completely independent binding, regardless of how many additional ligands are already bound. Numbers greater than one indicate positive cooperativity, while numbers less than one indicate negative cooperativity. The Hill coefficient was originally devised to explain the cooperative binding of oxygen to haemoglobin (a system which has a Hill coefficient of 2.8-3.0).
Hill equation:
- fraction of occupied sites where the ligand can bind to the active site of the receptor protein.
- free (unbound) ligand concentration
- Apparent dissociation constant derived from the law of mass action (equilibrium constant for dissociation)
- ligand concentration producing half occupation (ligand concentration occupying half of the binding sites), that is also the microscopic dissociation constant.
- Hill coefficient, describing cooperativity (or possibly other biochemical properties, depending on the context in which the Hill equation is being used)
Taking the reciprocal of both sides, rearranging, inverting again, and then taking the logarithm on both sides of the equation leads to an alternative formulation of the Hill equation:
When appropriate, the value of the Hill coefficient describes the cooperativity of ligand binding in the following way:
- - Positively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules increases.
- - Negatively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules decreases.
- - Noncooperative binding: The affinity of the enzyme for a ligand molecule is not dependent on whether or not other ligand molecules are already bound.
The Hill equation (as a relationship between the concentration of a compound adsorbing to binding sites and the fractional occupancy of the binding sites) is equivalent to the Langmuir equation.
See also
The Hill equation is related to the logistic function and is in some ways a logarithmic transform of it, i.e. when you plot the Hill function on a log scale it looks identical to a logistic function. This is particularly important if the range of concentrations that results in saturation does not vary over several orders of magnitude. In such a case the logistic function would be a more appropriate equation to model the behavior.
References
- ↑ A. V. Hill, "The possible effects of the aggregation of the molecules of hæmoglobin on its dissociation curves", J. Physiol., 40:iv-vii, 1910
- Dorland's Illustrated Medical Dictionary
- Lehninger Principles of Biochemistry, 4th edition, David L. Nelson & Michael M. Cox
- M. L. Coval, "Analysis of Hill interaction coefficients and the invalidity of the Kwon and Brown equation", J. Biol. Chem.', 245(23):6335–6336, 1970
- Donald Voet and Judith G. Voet, "Biochemistry"
- B. Mitavskiy, D. Chu and R. Zabet, "Models of transcription factor binding: Sensitivity of activation functions to model assumptions", Journal of Theoretical Biology, 257(3):419–429, 2009
This article uses material from the Wikipedia article Hill equation (biochemistry), which is released under the Creative Commons Attribution-ShareAlike Unported License 3.0.
![{\displaystyle \theta ={[L]^{n} \over K_{d}+[L]^{n}}={[L]^{n} \over (K_{A})^{n}+[L]^{n}}={1 \over ({K_{A} \over [L]})^{n}+1}}](https://wikimedia.org/api/rest_v1/media/math/render/png/9dcf71707c0d2aba2dd4d9b29aca9c6eaed6b162)
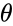 - fraction of occupied sites where the ligand can bind to the active site of the receptor protein.
- fraction of occupied sites where the ligand can bind to the active site of the receptor protein.
![{\displaystyle [L]}](https://wikimedia.org/api/rest_v1/media/math/render/png/c1eba88cad4b17de726ed2c779b29eecdf5819a2) - free (unbound) ligand concentration
- free (unbound) ligand concentration
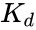 - Apparent dissociation constant derived from the
- Apparent dissociation constant derived from the 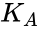 - ligand concentration producing half occupation (ligand concentration occupying half of the binding sites), that is also the microscopic dissociation constant.
- ligand concentration producing half occupation (ligand concentration occupying half of the binding sites), that is also the microscopic dissociation constant.
 - Hill coefficient, describing cooperativity (or possibly other biochemical properties, depending on the context in which the Hill equation is being used)
- Hill coefficient, describing cooperativity (or possibly other biochemical properties, depending on the context in which the Hill equation is being used)
![{\displaystyle \log \left({\theta \over 1-\theta }\right)=n\log {[L]}-\log {K_{d}}.}](https://wikimedia.org/api/rest_v1/media/math/render/png/656ffe54e5cc41117b525e4ced7a5a119a8314ab)
 - Positively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules increases.
- Positively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules increases.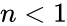 - Negatively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules decreases.
- Negatively cooperative binding: Once one ligand molecule is bound to the enzyme, its affinity for other ligand molecules decreases.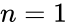 - Noncooperative binding: The affinity of the enzyme for a ligand molecule is not dependent on whether or not other ligand molecules are already bound.
- Noncooperative binding: The affinity of the enzyme for a ligand molecule is not dependent on whether or not other ligand molecules are already bound.