Stochastic modeling of reaction networks
Stochastic modeling of reaction networks is a framework for modeling the time evolution of chemical species when it is not reasonable to assume the individual chemical species can be averaged into a concentration. Since each reaction represents an inherently probabilistic event on a discrete state space (the number of molecules or each time), the resulting models are fundamentally stochastic in nature. They give rise to a continuous-time Markov chain.
Stochastic models for chemical reactions are particularly widespread in modeling of biochemical reactions occurring within or between cells, where the number of interacting species can typically be stated on the order of tens or hundreds. This stands in contrast to many industrial applications, where the order of the interacting species is typically large enough to justify the approximation
where is the number of the interacting species and is the volume of the reaction medium.
Several techniques are commonly used to analyze stochastic models of reaction networks, including generating sample trajectories (Gillespie's algorithm) and determining equations governing the time evolution of the network's probability distribution (chemical master equation).

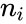 is the number of the
is the number of the 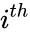 interacting species and
interacting species and 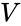 is the volume of the reaction medium.
is the volume of the reaction medium.