Finite escape time
A trajectory of a dynamical system is said to have finite escape time if for some . That is to say, the trajectory blows up to infinity (and ceases to exist) at a finite time in the future.
Finite escape time in mass action systems
Finite escape time can be exhibited by mass action systems. For example, consider the dynamical system
corresponding to the reactions and , with both rate constants equal to one and a positive initial concentration [1]. This system has solution which satisfies for . In other words, the solution blows up to infinity within a finite time.
It is worth noting that finite escape time is not simply the capacity of a trajectory to blow up. Consider the dynamical system
corresponding to the reaction with associated rate constant and a strictly positive initial concentration. The solution blows up but there is no point such that . Consequently, no trajectory of this mechanism exhibits finite escape time.
References
- ↑ Matthew D. Johnston, Topics in Chemical Reaction Network Theory, Ph.D. Thesis, University of Waterloo, 2011.
 of a dynamical system is said to have finite escape time if
of a dynamical system is said to have finite escape time if 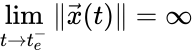 for some
for some  . That is to say, the trajectory blows up to infinity (and ceases to exist) at a finite time in the future.
. That is to say, the trajectory blows up to infinity (and ceases to exist) at a finite time in the future.
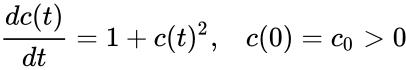
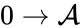 and
and  , with both rate constants equal to one and a positive initial concentration
, with both rate constants equal to one and a positive initial concentration 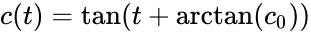 which satisfies
which satisfies 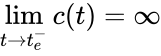 for
for 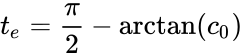 . In other words, the solution blows up to infinity within a finite time.
. In other words, the solution blows up to infinity within a finite time.
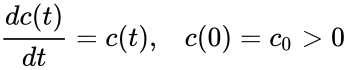
 with associated rate constant
with associated rate constant 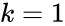 and a strictly positive initial concentration. The solution
and a strictly positive initial concentration. The solution 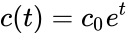 blows up but there is no point
blows up but there is no point 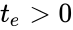 such that
such that