Indexing
The quantities of interest in the mathematical modeling of reaction networks can been indexed in a number of different ways. This is highlighted by the disparity between approaches which primarily emphasize the effect of reactions and those which emphasize the placement of complexes in the reaction graph. For example, notice that ambiguity arises when we attempt to track the complexes in the following reaction network:
On the left we have the reaction network represented as a list of elementary reactions whereas on the right we have the reaction graph of the network. Notice that, for instance, the complex corresponding to can be indexed three times as the reactant complex of the first reaction () and the product of the second and fourth reaction ( and ) or only once as a fixed node () with multiple adjacent reactions (one, two, and four). In the second setting, we index the reactions according to the fixed nodes between which they interact so that the first reaction would be corresponded to and the second and fourth reaction would be corresponded to for some and .
Reaction-centered indexing
In reaction-centered indexing, the reactions are numbered sequentially from where is the number of reactions. The complexes are indexed according to the reaction they appear in and whether they are reactant or product complex (product complexes are indicated with a prime, so that the product complex of the complex is denoted ). For mass-action systems, the rate constant associated with each reaction is assigned the index corresponding to the reaction, that is to say, we set , .
Using the reaction-centered indexing scheme, we represent a chemical reaction network as
where is the stoichiometric coefficient of the species in the reactant complexes of the reaction, and is the stoichiometric coefficient of the species in the product complex of the reaction. The complex vectors are given by and for .
For example, in the above example, we have
Complex-centered indexing
In complex-centered indexing, the complexes are indexed according to their stoichiometrically distinctiveness from . That is to say, each stoichiometrically distinct complex is assigned only one index, and one corresponding complex vector, regardless of whether it appears in just one or multiple reactions. The reactions are then indexed as ordered pairs depending on which stoichiometric distinct complexes the reaction connections and the direction of the connection. For mass-action systems, the rate constant associated with each reaction is assigned the indices corresponding to the complexes the reaction connects, that is to say, we set , , if .
Using the complex-centered indexing scheme, we represent a chemical reaction network as
where is the stoichiometric coefficient of the species in the complex. The complex vectors are given by for .
For example, in the above example, if we set , , and , we have
Conversion from reaction- to complex- centered indexing in mass-action systems
The dynamics of a mass-action system can be formulated in numerous equivalent forms. A primary difference between the representations is a result of the indexing scheme used and, in particular, the use of reaction- versus complex-centered indexing.
In the reaction-centered indexing scheme, it is most natural to represent a mass-action system as
where is the stoichiometric matrix and is the rate vector with entries .
In order to convert this expression into a form which utilizes complex-centered indexing, we re-index each rate constant , , to be where the reaction from the complex to the complex is the reaction in the reaction-centered indexing scheme. We now introduce two new matrices, and with entries defined as follows:
and
for . Recalling the complex matrix and the mass action vector , it follows that the matrices and decompose according to and so that we can re-write the mass-action system as
In order to further simplify the equations, we notice that the kinetic or Kirchhoff matrix is given by the product of the matrices and under the re-indexing of the rate constants from the reaction-centered to the complex-centered , i.e. .[1] It follows that
Example
For the above example, we can use the reaction-centered indexing to write the mass-action system as
Using the decomposition and as above, we have that
This can be put into the form
which after exchanging indices to the complex-centered form yields
References
- ↑ Karin Gatermann and Birkett Huber, A family of sparse polynomial systems arising in chemical reaction systems, J. Symbolic Comput., 33(3):275--305, 2002.
![{\displaystyle {\begin{array}{rclccc}{\mathcal {A}}_{1}&\;\longrightarrow \;&{\mathcal {A}}_{2}&{\mathcal {A}}_{1}\;\;\rightleftarrows \;\;{\mathcal {A}}_{2}\\[0.1cm]{\mathcal {A}}_{2}&\;\longrightarrow \;&{\mathcal {A}}_{1}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Longleftrightarrow \;\;\;\;\;\;\;\;\;\;&\nwarrow \;\;\;\;\;\swarrow \\[0.1cm]{\mathcal {A}}_{2}&\;\longrightarrow \;&{\mathcal {A}}_{3}+{\mathcal {A}}_{4}&{\mathcal {A}}_{3}+{\mathcal {A}}_{4}.\\[0.1cm]{\mathcal {A}}_{3}+{\mathcal {A}}_{4}&\;\longrightarrow \;&{\mathcal {A}}_{1}&&&\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/c17004225c2770705c37e6fb0321c3c19c9b286a)
![{\displaystyle {\vec {y}}=[1,0,0,0]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/cb6576299133bd46b12510eb9c78c104f90bd0bf) can be indexed three times as the reactant complex of the first reaction (
can be indexed three times as the reactant complex of the first reaction (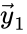 ) and the product of the second and fourth reaction (
) and the product of the second and fourth reaction (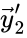 and
and 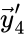 ) or only once as a fixed node (
) or only once as a fixed node (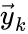 ) with multiple adjacent reactions (one, two, and four). In the second setting, we index the reactions according to the fixed nodes between which they interact so that the first reaction would be corresponded to
) with multiple adjacent reactions (one, two, and four). In the second setting, we index the reactions according to the fixed nodes between which they interact so that the first reaction would be corresponded to 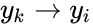 and the second and fourth reaction would be corresponded to
and the second and fourth reaction would be corresponded to 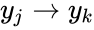 for some
for some  and
and 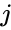 .
.
 where
where 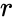 is the number of reactions. The complexes are indexed according to the reaction they appear in and whether they are reactant or product complex (product complexes are indicated with a prime, so that the product complex of the
is the number of reactions. The complexes are indexed according to the reaction they appear in and whether they are reactant or product complex (product complexes are indicated with a prime, so that the product complex of the 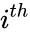 complex is denoted
complex is denoted 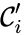 ). For mass-action systems, the rate constant associated with each reaction is assigned the index corresponding to the reaction, that is to say, we set
). For mass-action systems, the rate constant associated with each reaction is assigned the index corresponding to the reaction, that is to say, we set 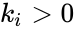 ,
, 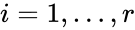 .
.
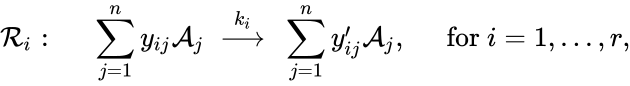
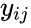 is the
is the 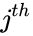 species in the reactant complexes of the
species in the reactant complexes of the 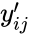 is the stoichiometric coefficient of the
is the stoichiometric coefficient of the ![{\displaystyle {\vec {y}}_{i}=[y_{i1},y_{i2},\ldots ,y_{in}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/6aadcee7673e704f500f57bb1b192131d96ee6b2) and
and ![{\displaystyle {\vec {y}}_{i}'=[y_{i1}',y_{i2}',\ldots ,y_{in}']^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/png/f6e5ab8a782590277065147b37b27a7590cc02c1) for
for ![{\displaystyle {\vec {y}}_{1}=\left[{\begin{array}{c}1\\0\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{1}'=\left[{\begin{array}{c}0\\1\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{2}=\left[{\begin{array}{c}0\\1\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{2}'=\left[{\begin{array}{c}1\\0\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{3}=\left[{\begin{array}{c}0\\1\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{3}'=\left[{\begin{array}{c}0\\0\\1\\1\end{array}}\right],\;\;\;{\vec {y}}_{4}=\left[{\begin{array}{c}0\\0\\1\\1\end{array}}\right],\;\;\;{\vec {y}}_{4}'=\left[{\begin{array}{c}1\\0\\0\\0\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/3bf7cf5f1b2beba6af73416a6973996c6321b6ce)
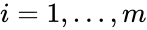 . That is to say, each stoichiometrically distinct complex is assigned only one index, and one corresponding complex vector, regardless of whether it appears in just one or multiple reactions. The reactions are then indexed as ordered pairs depending on which stoichiometric distinct complexes the reaction connections and the direction of the connection. For mass-action systems, the rate constant associated with each reaction is assigned the indices corresponding to the complexes the reaction connects, that is to say, we set
. That is to say, each stoichiometrically distinct complex is assigned only one index, and one corresponding complex vector, regardless of whether it appears in just one or multiple reactions. The reactions are then indexed as ordered pairs depending on which stoichiometric distinct complexes the reaction connections and the direction of the connection. For mass-action systems, the rate constant associated with each reaction is assigned the indices corresponding to the complexes the reaction connects, that is to say, we set 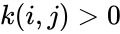 ,
, 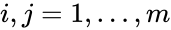 , if
, if  .
.

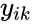 is the
is the 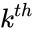 species in the
species in the 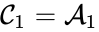 ,
, 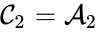 , and
, and 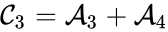 , we have
, we have
![{\displaystyle {\vec {y}}_{1}=\left[{\begin{array}{c}1\\0\\0\\0\end{array}}\right],\;\;\;\;\;{\vec {y}}_{2}=\left[{\begin{array}{c}0\\1\\0\\0\end{array}}\right],\;\;\;\;\;{\vec {y}}_{3}=\left[{\begin{array}{c}0\\0\\1\\1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/2e73828f49bc9f52adb5bcecdfae6753f83b0e1f)
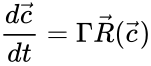
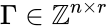 is the
is the 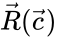 is the rate vector with entries
is the rate vector with entries 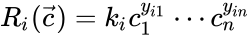 .
.
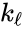 ,
, 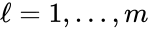 , to be
, to be 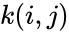 where the reaction from the
where the reaction from the 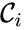 to the
to the 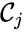 is the
is the 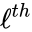 reaction in the reaction-centered indexing scheme. We now introduce two new matrices,
reaction in the reaction-centered indexing scheme. We now introduce two new matrices, 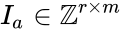 and
and 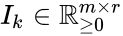 with entries defined as follows:
with entries defined as follows:
![{\displaystyle [I_{a}]_{i\ell }=\left\{{\begin{array}{ll}1,\;\;\;\;\;&{\mbox{if }}{\mathcal {C}}_{i}{\mbox{ is the product complex of the }}\ell ^{th}{\mbox{ reaction}}\\-1,\;\;\;\;\;&{\mbox{if }}{\mathcal {C}}_{i}{\mbox{ is the reactant complex of the }}\ell ^{th}{\mbox{ reaction}}\\0,&{\mbox{otherwise}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/png/7bccfbd8ab16983a809135f643a2ad88ceb087c2)
![{\displaystyle [I_{k}]_{\ell i}=\left\{{\begin{array}{ll}k_{\ell },\;\;\;\;\;&{\mbox{if }}{\mathcal {C}}_{i}{\mbox{ is the reactant complex of the }}\ell ^{th}{\mbox{ reaction}}\\0,&{\mbox{otherwise}}\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/png/026de00c60752d766f2fa446ba3eeb22dd6d3a74)
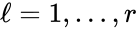 . Recalling the
. Recalling the  and the
and the 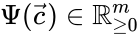 , it follows that the matrices
, it follows that the matrices 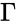 and
and 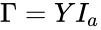 and
and 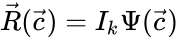 so that we can re-write the mass-action system as
so that we can re-write the mass-action system as
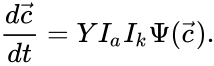
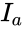 and
and 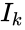 under the re-indexing of the rate constants from the reaction-centered
under the re-indexing of the rate constants from the reaction-centered 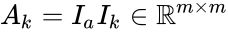 .
.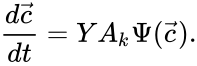
![{\displaystyle {\frac {d{\vec {c}}}{dt}}=\Gamma {\vec {R}}({\vec {c}})=\left[{\begin{array}{cccc}-1&1&0&1\\1&-1&-1&0\\0&0&1&-1\\0&0&1&-1\end{array}}\right]\left[{\begin{array}{c}k_{1}c_{1}\\k_{2}c_{2}\\k_{3}c_{2}\\k_{4}c_{3}c_{4}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/5146e233ecfc0da50e1e73b66e0ddaea4722e4ed)
![{\displaystyle {\frac {d{\vec {c}}}{dt}}=YI_{a}I_{k}\Psi ({\vec {c}})=\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\\0&0&1\end{array}}\right]\left[{\begin{array}{cccc}-1&1&0&1\\1&-1&-1&0\\0&0&1&-1\end{array}}\right]\left[{\begin{array}{ccc}k_{1}&0&0\\0&k_{2}&0\\0&k_{3}&0\\0&0&k_{4}\end{array}}\right]\left[{\begin{array}{ccc}c_{1}\\c_{2}\\c_{3}c_{4}.\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/737ede4bc79e69bb19cb2bc9d12da9641e3132e8)
![{\displaystyle {\frac {d{\vec {c}}}{dt}}=\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\\0&0&1\end{array}}\right]\left[{\begin{array}{ccc}-k_{1}&k_{2}&k_{4}\\k_{1}&-k_{2}-k_{3}&0\\0&k_{3}&-k_{4}\end{array}}\right]\left[{\begin{array}{ccc}c_{1}\\c_{2}\\c_{3}c_{4}.\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/afb69ea126e474ade4a65e98f03f33db940c0bb6)
![{\displaystyle {\frac {d{\vec {c}}}{dt}}=YA_{k}\Psi ({\vec {c}})=\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\\0&0&1\end{array}}\right]\left[{\begin{array}{ccc}-k(1,2)&k(2,1)&k(3,1)\\k(1,2)&-k(2,1)-k(2,3)&0\\0&k(2,3)&-k(3,1)\end{array}}\right]\left[{\begin{array}{ccc}c_{1}\\c_{2}\\c_{3}c_{4}.\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/0b9e41e9f55260f8cf8c4b0d99eab0b421cd0f40)