Reaction graph
The reaction graph of a chemical reaction network is given by the directed graph G(V,E) where the set of vertices V are given by the set of stoichiometrically distinct complexes , and the directed edges are given by the reaction set . The reaction graph has been shown to have many important connections with the dynamics of a chemical reaction network under a variety of kinetic assumptions [1][2][3][4][5][6][7].
Terminology
The terminology related to the reaction graphs of chemical reaction networks is varied but certain important concepts are recurrent. The terminology is primarily derived from graph theory, with the exception that the vertices V are called complexes and the directed edges E are called reactions.
A key feature is how complexes are connected to one another, the most immediate notion of which is the direct connections, that is to say, the reactions themselves. To this end, a complex is said to react to a complex if and a complex is to said to react from if . This terminology allows to characterize the source complexes of a chemical reaction network as the complexes which react to other complexes. Source complexes are particularly important in chemical reaction network theory because the rate of a reaction is determined uniquely by the stoichiometry of the reactant complex and the kinetic assumption (i.e. it does not depend on the product complex).
We can also define concepts which extend the notions of connectedness to chains which extend through intermediate complexes. A complex is said to be connected to a complex if there exists a sequence of complexes such that , such that , , and either reacts to or reacts from for all . The notion of connectedness does not imply directionality of the intermediate reactions and, consequently, is not a very strong condition. The strong notion which is includes directionality is that of a path. We will say that there is a path from to if there exists a sequence of complexes such that , such that , , and reacts to for all .
Consider the network
We can see that the complexes , , and are all connected to one another, but paths do not exist between all complexes. In particular, there is no path from to or , or from to . The complexes , , and are not connected to the complexes and , and consequently no path may exist between them.
Linkage classes
A set is called a linkage class if and implies and are connected, but and implies and are not connected. That is to say, a linkage class is a maximal set of connected complexes. The set of linkage classes of a network is denoted where for are the individual linkage classes and is the number of distinct linkage classes in the network.
Linkage classes form a complete partition of the complex set . That is to say, every complex belongs to exactly one linkage class. This can be expressed mathematically with the conditions
For the network given above, we have the linkage classes and . We notice that this represents a complex partition of the complex set, and that the linkage classes themselves do not recognize directionality of reactions (i.e. we do not care that there is no path from to , for instance).
Cycles
Of particular interest are paths which lead back to their original complex. If they do so without repeating any intermediary complexes, the resulting path is called a cycle. Formally, we can the that sequence of complexes is a cycle of length l if , no other complex is repeated, and for all . That is to say, the set is a cycle if
For example, if we consider a chemical reaction network with reaction graph given by
we observe that the sequence of complexes corresponds to a cycle, as does the sequence . We also notice that the complex is not the part of any cycle.
The decomposition of weakly reversible chemical reaction networks into cycles is a key element of the arguments used in the fundamental results of Fritz Horn and Roy Jackson regarding complex balanced mass action systems [1].
Reversibility
A particularly strong notion of connectedness in a reaction graph is the notion of reversibility. A chemical reaction network is said to reversible if implies . That is to say, each reaction in the network can be corresponded to a inverse reaction. It is common to refer to one reaction as the forward reaction and the other as the backward reaction. It is also common in mass-action systems to assign the rate constants associated with a reversible pair a single index, and then differential between the forward and backward step (e.g. and , and , etc.).
For example, the following reaction network is reversible
Notice that reversibility is a local property and does not imply a connection between all of the complexes in the network.
Reversible chemical reaction networks are known to be strongly related to the capacity of the corresponding mass-action systems to permit detailed balanced equilibrium concentrations [8].
Weak reversibility
A weaker notion of connectedness in a reaction graph is the notion of weak reversibility. A chemical reaction network is said to weakly reversible if the existence of a path from to implies the existence of a path from to . That is to say, a network is weakly reversible if, no matter where you go, you can always get back to where you started. Reversible networks are a subset of weakly reversible networks.
For example, consider the chemical reaction network
The network is not reversible but it is weakly reversible. It is worth noting that this network is weakly reversible even though not every complex is connected to every other complex.
Weakly reversible chemical reaction networks are known to be strongly related to the capacity of the corresponding mass action systems to permit complex-balanced equilibrium concentrations [1] [2] [3].
The notion of weak reversibility may also be applied to subsets of a network. In particular, a set is said to be strongly connected if implies there is a path from to , and if no other complexes may be added to the set while holding this property. In other words, a subset of complexes is strongly connected if it is a maximal set with a path between every complex in the set. Furthermore, we will say that a strongly connected component is terminal if there does not exist a reaction for any and . In other words, the component is terminal if there is no reaction leading out of the set.
Consider the example
This network is not weakly reversible, since we can go from to but there is no path back, but the complex sets and are strongly connected. It is clear, however, that only is terminal.
Deficiency
The deficiency is property of a chemical reaction network which relates several graph theoretic quantities derived from the reaction graph. It was introduced by Martin Feinberg in 1972 [3] and has been widely studied since [9][10][11][12].
The deficiency of a chemical reaction network is typically defined as , where is the number of stoichiometrically distinct complexes, is the number of linkage classes, and is the dimension of the stoichiometric subspace. The deficiency is known to be a non-negative integer value [3]. It is a specialized measure of the linear independence of the reaction vectors of a network.
For example, consider the networks given by:
For we have stoichiometrically distinct complexes, linkage classes, and a stoichiometric subspace of dimension , so that the deficiency is . The network is similar except that the dimension of the stoichiometric subspace is so that . The network has , , and so that .
Many dynamical results are known to hold for mass-action systems with particular deficiency values. In particular, weakly reversible deficiency zero mass-action systems are known to be complex balanced (and therefore exhibit locally stable dynamics) for all rate constant values [3] [2]. Other deficiency-based results have been derived for networks which are not weakly reversible and for which high deficiency values are attained.
An alternative definition of the deficiency is [13][14]. Since the linear portion of the general kinetic system allows any equilibrium condition to be stated as the kernel condition, this formulation most clearly demonstrates the difference between complex balanced equilibrium concentrations (those satisfying ) and non-complex balanced equilibrium concentrations (those satisfying ). It is known that the two definitions coincide if every linkage class contains exactly one terminal strongly linked component, which in particular is true if the network is weakly reversible (Proposition 5.1 [13]). In general, we have .
See also:
References
- ↑ 1.0 1.1 1.2 Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:81--116, 1972
- ↑ 2.0 2.1 2.2 Fritz Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal., 49:172--186, 1972
- ↑ 3.0 3.1 3.2 3.3 3.4 Martin Feinberg, Complex balancing in general kinetic systems, Arch. Ration. Mech. Anal., 49:187--194, 1972
- ↑ Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: I. the deficiency zero and deficiency one theorems, Chem. Eng. Sci., 42(10):2229--2268, 1987
- ↑ Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: II. multiple steady states for networks of deficiency one, Chem. Eng. Sci., 43(1):1--25, 1988
- ↑ Gheorghe Craciun, Alicia Dickenstein, Anne Shiu, and Bernd Sturmfels, Toric dynamical systems, J. Symbolic Comput., 44(11):1551--1565, 2009
- ↑ Gheorghe Craciun, Casian Pantea, and Fedor Nazarov, Persistence and permanence of mass-action and power-law dynamical systems, to appear SIAM J. Appl. Math., 2012
- ↑ Aizik I. Vol'pert and Sergei I. Hudjaev, Analysis in Classes of Discontinuous Functions and Equations of Mathematical Physics, Martinus Nijhoff Publishers, Dordrecht, Netherlands, 1985
- ↑ Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: I. the deficiency zero and deficiency one theorems, Chem. Eng. Sci., 42(10):2229--2268, 1987
- ↑ Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: II. multiple steady states for networks of deficiency one, Chem. Eng. Sci., 43(1):1--25, 1988
- ↑ Martin Feinberg, The existence and uniqueness of steady states for a class of chemical reaction networks, Arch. Ration. Mech. Anal., 132:311-370, 1995
- ↑ Martin Feinberg, Multiple steady states for chemical reaction networks of deficiency one, Arch. Ration. Mech. Anal., 132:371--406, 1995
- ↑ 13.0 13.1 Jeremy Gunawardena, Chemical reaction network theory for in-silico biologists, 2003
- ↑ Stefan Muller and George Regensburger, Generalized Mass Action Systems: Complex Balancing Equilibria and Sign Vectors of the Stoichiometric and Kinetic-Order Subspaces, available on the arXiv at arXiv:1209.6488
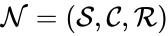 is given by the directed graph G(V,E) where the set of vertices V are given by the set of stoichiometrically distinct complexes
is given by the directed graph G(V,E) where the set of vertices V are given by the set of stoichiometrically distinct complexes  , and the directed edges are given by the reaction set
, and the directed edges are given by the reaction set 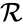 . The reaction graph has been shown to have many important connections with the dynamics of a
. The reaction graph has been shown to have many important connections with the dynamics of a 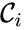 is said to react to a complex
is said to react to a complex 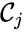 if
if  and a complex
and a complex 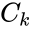 if
if 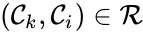 . This terminology allows to characterize the source complexes of a chemical reaction network as the complexes which react to other complexes. Source complexes are particularly important in chemical reaction network theory because the rate of a reaction is determined uniquely by the stoichiometry of the reactant complex and the kinetic assumption (i.e. it does not depend on the product complex).
. This terminology allows to characterize the source complexes of a chemical reaction network as the complexes which react to other complexes. Source complexes are particularly important in chemical reaction network theory because the rate of a reaction is determined uniquely by the stoichiometry of the reactant complex and the kinetic assumption (i.e. it does not depend on the product complex).
 ,
, 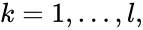 such that
such that  ,
, 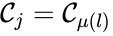 , and
, and 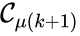 for all
for all  . The notion of connectedness does not imply directionality of the intermediate reactions and, consequently, is not a very strong condition. The strong notion which is includes directionality is that of a path. We will say that there is a path from
. The notion of connectedness does not imply directionality of the intermediate reactions and, consequently, is not a very strong condition. The strong notion which is includes directionality is that of a path. We will say that there is a path from ![{\displaystyle {\begin{array}{cc}{\mathcal {C}}_{1}\;\longrightarrow \;{\mathcal {C}}_{2}&\\[0.1cm]\searrow \;\;\;\;\swarrow &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathcal {C}}_{4}\;\;\rightleftarrows \;\;{\mathcal {C}}_{5}.\\[0.1cm]{\mathcal {C}}_{3}&\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/2e3807022e7c384c69ff80584675757338a6e966)
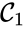 ,
, 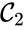 , and
, and 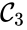 are all connected to one another, but paths do not exist between all complexes. In particular, there is no path from
are all connected to one another, but paths do not exist between all complexes. In particular, there is no path from 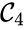 and
and 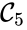 , and consequently no path may exist between them.
, and consequently no path may exist between them.
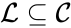 is called a linkage class if
is called a linkage class if 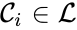 and
and 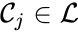 implies
implies 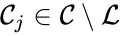 implies
implies 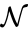 is denoted
is denoted 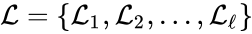 where
where 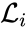 for
for 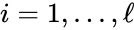 are the individual linkage classes and
are the individual linkage classes and 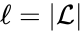 is the number of distinct linkage classes in the network.
is the number of distinct linkage classes in the network.
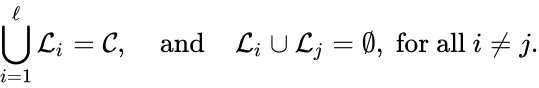
 and
and 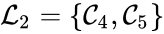 . We notice that this represents a complex partition of the complex set, and that the linkage classes themselves do not recognize directionality of reactions (i.e. we do not care that there is no path from
. We notice that this represents a complex partition of the complex set, and that the linkage classes themselves do not recognize directionality of reactions (i.e. we do not care that there is no path from 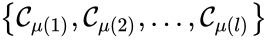 is a cycle of length l if
is a cycle of length l if 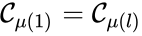 , no other complex is repeated, and
, no other complex is repeated, and 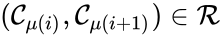 for all
for all  . That is to say, the set is a cycle if
. That is to say, the set is a cycle if
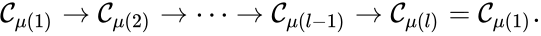
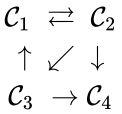
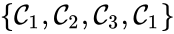 corresponds to a cycle, as does the sequence
corresponds to a cycle, as does the sequence 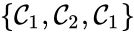 . We also notice that the complex
. We also notice that the complex 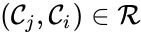 . That is to say, each reaction in the network can be corresponded to a inverse reaction. It is common to refer to one reaction as the forward reaction and the other as the backward reaction. It is also common in mass-action systems to assign the rate constants associated with a reversible pair a single index, and then differential between the forward and backward step (e.g.
. That is to say, each reaction in the network can be corresponded to a inverse reaction. It is common to refer to one reaction as the forward reaction and the other as the backward reaction. It is also common in mass-action systems to assign the rate constants associated with a reversible pair a single index, and then differential between the forward and backward step (e.g.  and
and 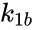 ,
, 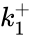 and
and  , etc.).
, etc.).
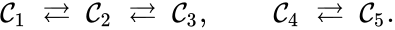
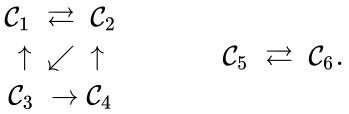
 is said to be strongly connected if
is said to be strongly connected if 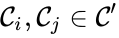 implies there is a path from
implies there is a path from 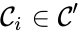 and
and 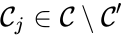 . In other words, the component is terminal if there is no reaction leading out of the set.
. In other words, the component is terminal if there is no reaction leading out of the set.

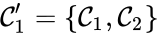 and
and  are strongly connected. It is clear, however, that only
are strongly connected. It is clear, however, that only 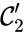 is terminal.
is terminal.
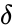 of a chemical reaction network is typically defined as
of a chemical reaction network is typically defined as 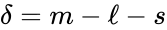 , where
, where 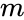 is the number of stoichiometrically distinct
is the number of stoichiometrically distinct  is the number of
is the number of 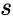 is the dimension of the
is the dimension of the ![{\displaystyle {\begin{array}{cccccc}&\emptyset \;\longrightarrow \;{\mathcal {A}}_{1}&&2{\mathcal {A}}_{1}\;\longrightarrow \;2{\mathcal {A}}_{2}&&2{\mathcal {A}}_{1}+{\mathcal {A}}_{2}\;\longrightarrow \;3{\mathcal {A}}_{1}\\[0.1cm]{\mathcal {N}}_{1}:\;\;\;&\nwarrow \;\;\;\;\swarrow &\;\;\;\;\;{\mathcal {N}}_{2}:\;\;\;&\nwarrow \;\;\;\;\;\swarrow &\;\;\;\;\;{\mathcal {N}}_{3}:\;\;\;&\uparrow \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\downarrow \\[0.1cm]&{\mathcal {A}}_{2}&&{\mathcal {A}}_{1}+{\mathcal {A}}_{2}&&3{\mathcal {A}}_{2}\;\longleftarrow \;{\mathcal {A}}_{1}+2{\mathcal {A}}_{2}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/af52b892f9f54802cad2a6f53bdb88cd77df617d)
 we have
we have 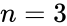 stoichiometrically distinct complexes,
stoichiometrically distinct complexes, 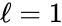 linkage classes, and a stoichiometric subspace of dimension
linkage classes, and a stoichiometric subspace of dimension 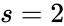 , so that the deficiency is
, so that the deficiency is 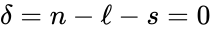 . The network
. The network 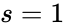 so that
so that 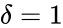 . The network
. The network 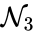 has
has 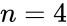 ,
, 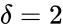 .
.

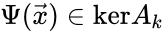 ) and non-complex balanced equilibrium concentrations (those satisfying
) and non-complex balanced equilibrium concentrations (those satisfying 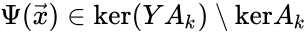 ). It is known that the two definitions coincide if every
). It is known that the two definitions coincide if every 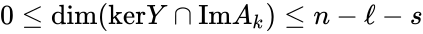 .
.