Stoichiometry
Stoichiometry in the mathematical modeling of chemical reactions is the manner in which the quantities of reactants and products involved in chemical reactions are tracked. Of particular interest is the number of molecules require to catalyze a reaction and the number produced by a reaction. For physical reasons, the stoichiometric quantities are typically assumed to be whole numbers.
In a general reaction of the form , a vector is assigned to the reactant and product complexes according to and . For example, in the reaction network
the following vectors are assigned
to indicate that the reactant complex of the first reaction consists of one element of the first species and second species, the product complex of the first reaction consists of one element of the third species, and so on.
Complex matrix
The complex matrix is the matrix with columns given by the stoichiometrically distinct complexes. For the reaction network given above we have
Stoichiometric subspace
The stoichiometric subspace is given by the span of the reaction vectors , . In other words, we define
The dimension of the stoichiometric subspace is commonly denoted . For the network above we have
In other words, there is a net loss of one molecule of species one and two and a net gain of one molecule of species three as a result of reaction one, and a loss of two molecules of species three and gain of one molecule of species four as a result of reaction two. It follows that
and the dimension is .
Stoichiometric matrix
The stoichiometric matrix is the matrix with the column given by the reaction vector . For the network above we have
Stoichiometric compatibility classes
The stoichiometric compatibility classes of a chemical reaction network are the sets . They are affine translations of the stoichiometric subspaces and their interiors are locally homeomorphic to the Euclidean space of dimension .
Stoichiometric compatibility classes arise from the general kinetic form of a chemical reaction network. Integrating directly gives
for all . When , it follows that solutions may not wander freely about the positive orthant ; rather, they are restricted to a translation (determined by the initial condition) of stoichiometric subspace. With modest assumptions of the form of the rate functions , it follows that for all [1]. For the above network, even though the system is five-dimensional, trajectories remain in two-dimensional translations of .
References
- ↑ Aizik I. Vol'pert and Sergei I. Hudjaev, Analysis in Classes of Discontinuous Functions and Equations of Mathematical Physics, Martinus Nijhoff Publishers, Dordrecht, Netherlands, 1985.
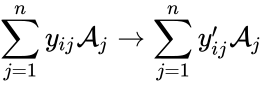 , a vector is assigned to the reactant and product
, a vector is assigned to the reactant and product ![{\displaystyle {\vec {y}}_{i}=[y_{i1},y_{i2},\ldots ,y_{in}]^{T}\in \mathbb {Z} _{\geq 0}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/png/e2242633d26bc267c996b6b175b30c8d7c923e56) and
and ![{\displaystyle {\vec {y}}_{i}'=[y_{i1}',y_{i2}',\ldots ,y_{in}']^{T}\in \mathbb {Z} _{\geq 0}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/png/fa6f8b64572f7a239d875344393cd4dde1a1aa7e) . For example, in the reaction network
. For example, in the reaction network
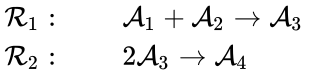
![{\displaystyle {\vec {y}}_{1}=\left[{\begin{array}{c}1\\1\\0\\0\end{array}}\right],\;\;\;{\vec {y}}_{1}'=\left[{\begin{array}{c}0\\0\\1\\0\end{array}}\right],\;\;\;{\vec {y}}_{2}=\left[{\begin{array}{c}0\\0\\2\\0\end{array}}\right],{\vec {y}}_{2}'=\left[{\begin{array}{c}0\\0\\0\\1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/b3b026edac6776011593ef158385764c21557cb7)
 is the matrix with columns given by the stoichiometrically distinct
is the matrix with columns given by the stoichiometrically distinct ![{\displaystyle Y=\left[{\begin{array}{cccc}1&0&0&0\\1&0&0&0\\0&1&2&0\\0&0&0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/5d2ce63e733888e9aacf98605d24fcc01c8334d2)
 is given by the span of the reaction vectors
is given by the span of the reaction vectors 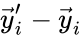 ,
, 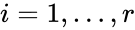 . In other words, we define
. In other words, we define
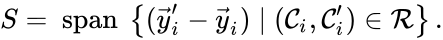
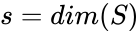 . For the network above we have
. For the network above we have
![{\displaystyle {\vec {y}}_{1}'-{\vec {y}}_{1}=\left[{\begin{array}{c}0\\0\\1\\0\end{array}}\right]-\left[{\begin{array}{c}1\\1\\0\\0\end{array}}\right]=\left[{\begin{array}{c}-1\\-1\\1\\0\end{array}}\right]\;\;\;{\mbox{and}}\;\;\;{\vec {y}}_{2}'-{\vec {y}}_{2}=\left[{\begin{array}{c}0\\0\\0\\1\end{array}}\right]-\left[{\begin{array}{c}0\\0\\2\\0\end{array}}\right]=\left[{\begin{array}{c}0\\0\\-2\\1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/4622f46f4d093634feba5cb2d762a89ff03d40c0)
![{\displaystyle S={\mbox{span}}\left\{\left[{\begin{array}{c}-1\\-1\\1\\0\end{array}}\right],\left[{\begin{array}{c}0\\0\\-2\\1\end{array}}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/png/20041fb003c338bce7c51e821c47ae641e0d9e23)
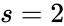 .
.
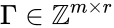 is the matrix with the
is the matrix with the 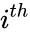 column given by the
column given by the ![{\displaystyle \Gamma =\left[{\begin{array}{cc}-1&0\\-1&0\\1&-2\\0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/png/a4122dcea1991c4a2e1b88b6e83695f2febbfdfa)
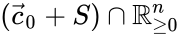 . They are affine translations of the stoichiometric subspaces
. They are affine translations of the stoichiometric subspaces 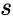 .
.

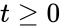 . When
. When 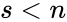 , it follows that solutions
, it follows that solutions 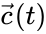 may not wander freely about the positive orthant
may not wander freely about the positive orthant 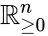 ; rather, they are restricted to a translation (determined by the initial condition) of stoichiometric subspace. With modest assumptions of the form of the rate functions
; rather, they are restricted to a translation (determined by the initial condition) of stoichiometric subspace. With modest assumptions of the form of the rate functions 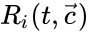 , it follows that
, it follows that 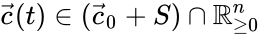 for all
for all