Persistence and the Global Attractor Conjecture
Persistence is a concept from population dynamics. In words, a model of species interactions (e.g. predator-prey) is persistent if, given an initial condition where all species have non-zero population, none of the species can become extinct. The meaning in chemical reaction network theory is analogous: a CRN model is called persistent if, given an initial condition where all chemical species have non-zero concentration, none of the species can be completely "used up", i.e. none of their concentrations can tend to zero. In mathematical terms, a CRN model is persistent if
where denotes the omega limit set of .
The persistence conjecture
Feinberg - 1987
Given a chemical reaction network system, assume:
- All reactions follow mass action kinetics,
- The network is weakly reversible and
- Each trajectory remains bounded.
Then the system is persistent.
Counterexample for power law kinetics
The assumption that all reactions obey the law of mass action is an essential part of the conjecture. Consider the following simple example network:
Let represent the concentrations of and respectively. It is easy to demonstrate that cannot tend to zero under standard kinetic assumptions. Note also that , where is a constant, and that all trajectories are bounded as a result. Under mass action kinetics,
For , the second term dominates, and so , implying that the system is persistent. Now consider the same system under more general kinetics, where the right-to-left reaction rate has been replaced by more general power law kinetics:
In this case, for the term dominates, and so , meaning that the system is not persistent.
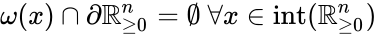
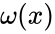 denotes the omega limit set of
denotes the omega limit set of  .
.
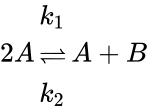
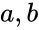 represent the concentrations of
represent the concentrations of  and
and  respectively. It is easy to demonstrate that
respectively. It is easy to demonstrate that  cannot tend to zero under standard kinetic assumptions. Note also that
cannot tend to zero under standard kinetic assumptions. Note also that 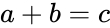 , where
, where 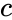 is a constant, and that all trajectories are bounded as a result. Under mass action kinetics,
is a constant, and that all trajectories are bounded as a result. Under mass action kinetics,
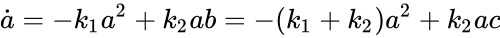
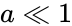 , the second term
, the second term 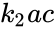 dominates, and so
dominates, and so 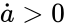 , implying that the system is persistent. Now consider the same system under more general kinetics, where the right-to-left reaction rate has been replaced by more general power law kinetics:
, implying that the system is persistent. Now consider the same system under more general kinetics, where the right-to-left reaction rate has been replaced by more general power law kinetics:
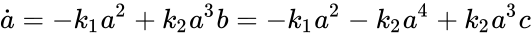
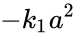 dominates, and so
dominates, and so 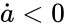 , meaning that the system is not persistent.
, meaning that the system is not persistent.