Deficiency theory
Deficiency theory in chemical reaction network theory encapsulates methods by which the network parameter known as the deficiency is related to the dynamics of the corresponding kinetic systems under some kinetic assumption. The majority of deficiency results pertain to mass action systems.
The notion of the deficiency of a chemical reaction network was introduced in 1972 by Fritz Horn[1] and Martin Feinberg[2] primarily as a way to characterize mass action systems which permitted complex balanced equilibrium concentrations. This basis has since been expanded upon to characterize the equilibrium set of systems for which the underlying network is not weakly reversible (a requirement of complex balanced systems) and for which the network has a nonzero deficiency value.
Deficiency zero theorem
The best known and oldest deficiency result is the Deficiency Zero Theorem. The following theorem was proved by Fritz Horn in 1972 (Theorem 4A[1]):
- Deficiency Zero Theorem
- A mass action system is complex balanced for every set of positive rate constants if and only if it is weakly reversible and has a deficiency of zero.
A more popular formulation of the theorem, which makes use of known results about complex balanced systems (Lemma 4B and Theorem 6A[3]), is the following:
- Deficiency Zero Theorem
- Consider a mass action system for which the underlying chemical reaction network is weakly reversible and deficiency zero. Then, for all choices of rate constants, the system has exactly one equilibrium concentration in each positive stoichiometric compatibility class and that equilibrium concentration is locally asymptotically stable.
The strength of the Deficiency Zero Theorem is that it gives strong restrictions on the dynamics and equilibrium set of the kinetic system under mass action kinetics based only on properties of the network's reaction graph. That is to say, we need only compute the three graph theoretic quantities which compose the deficiency (the number of stoichiometrically distinct complexes , the number of linkage classes , and the dimension of the stoichiometric subspace ) and establish weak reversibility in order to determine the very strong dynamic regularity guaranteed by complex balancing of equilibrium concentrations. Furthermore, this strong regularity is guaranteed regardless of the kinetic parameters.
Consider the following example (Example 3.4.2[4]):
It is clear that the system has stoichiometric distinct complexes, linkage classes, and is weakly reversible. It remains only to check the dimension of the stoichiometric subspace . We can see that we have
It follows that so that the deficiency is given by . Since this is a weakly reversible deficiency zero network, it follows that any corresponding mass action system is complex balanced, and therefore exhibits locally stable dynamics, for all rate constant choices. It is important to notice that this dynamical result is guaranteed to hold even though we have only computed quantities related underlying network's reaction graph.
Deficiency one theorem
The following well-known deficiency result was proved by Martin Feinberg in 1995[5]:
- Deficiency One Theorem
- Consider a chemical reaction network with deficiency and linkage classes. Let , denote the deficiencies of the individual linkage classes considered as their own networks. Suppose the following conditions:
1. for all ,
2. , and
3. each linkage class contains a single terminal strongly linked component.
Then, if a mass action system corresponding to the network with a specified rate set admits a positive equilibrium concentration, there exists precisely one equilibrium concentration in each positive stoichiometric compatibility class. Furthermore, if the network is weakly reversible, every mass action system permitted by the network has a positive equilibrium.
This result applied to networks for which the individual deficiencies of each linkage class is small (i.e. zero or one) and consistent with the overall deficiency (i.e. they add up). It is worth noting that, in spite of the name given to the theorem, the deficiency of the network in consideration need not be one, and that many deficiency one networks do not fall within the theorem's scope. The deficiency one requirement is a requirement on the individual linkage classes, not of the entire network. For instance, consider the futile cycle enzyme example[6]
This network has stoichiometrically distinct complexes, linkage classes, and a dimensional stoichiometric subspace to give a deficiency of . The deficiency one theorem may not be applied, however, because the deficiency of each linkage class is , so that .
Deficiency one algorithm
The Deficiency one algorithm is an algorithm capable of determining whether a regular chemical reaction network with a deficiency of one has the capacity for multiple positive steady states within a single stoichiometric compatibility class. It was first published by Martin Feinberg in 1988[7].
A chemical reaction network is regular if it satisfies the following conditions:
1. The reaction vectors are positively dependent, i.e. there is a set of positive values such that ,
2. Every linkage class contains only one terminal strongly connected component, and
3. Each pair of adjacent complexes in a terminal strongly connected component is a cut pair, i.e. removing the reactions between the adjacent complexes separates the linkage class into two linkage classes.
References
- ↑ 1.0 1.1 Fritz Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal., 49:172--186, 1972
- ↑ Martin Feinberg, Complex balancing in general kinetic systems, Arch. Ration. Mech. Anal., 49:187--194, 1972
- ↑ Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:81--116, 1972.
- ↑ Matthew D. Johnston, Topics in chemical reaction network theory, Ph.D. Thesis, University of Waterloo, 2011.
- ↑ Martin Feinberg, The existence and uniqueness of steady states for a class of chemical reaction networks, Arch. Ration. Mech. Anal., 132:311-370, 1995.
- ↑ Liming Wang and Eduardo Sontag, On the number of steady states in a multiple futile cycle, J. Math. Biol., 57(1):29--52, 2008.
- ↑ * Martin Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors: II. multiple steady states for networks of deficiency one, Chem. Eng. Sci., 43(1):1--25, 1988.
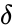 (the number of stoichiometrically distinct
(the number of stoichiometrically distinct  , the number of
, the number of  , and the dimension of the
, and the dimension of the 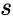 ) and establish
) and establish 
 stoichiometric distinct complexes,
stoichiometric distinct complexes, 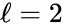 linkage classes, and is weakly reversible. It remains only to check the dimension of the stoichiometric subspace
linkage classes, and is weakly reversible. It remains only to check the dimension of the stoichiometric subspace ![{\displaystyle S={\mbox{span}}\left\{\left[{\begin{array}{c}-1\\1\\0\\0\end{array}}\right],\left[{\begin{array}{c}0\\-1\\1\\1\end{array}}\right],\left[{\begin{array}{c}1\\0\\-1\\-1\end{array}}\right],\left[{\begin{array}{c}-2\\0\\2\\0\end{array}}\right],\left[{\begin{array}{c}2\\0\\-2\\0\end{array}}\right]\right\}={\mbox{span}}\left\{\left[{\begin{array}{c}-1\\1\\0\\0\end{array}}\right],\left[{\begin{array}{c}0\\-1\\1\\1\end{array}}\right],\left[{\begin{array}{c}-2\\0\\2\\0\end{array}}\right]\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/png/06d885017a96c28ecc80ba2c31a7963d58b07af0)
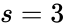 so that the deficiency is given by
so that the deficiency is given by 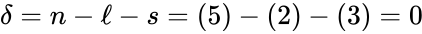 . Since this is a weakly reversible deficiency zero network, it follows that any corresponding mass action system is complex balanced, and therefore exhibits
. Since this is a weakly reversible deficiency zero network, it follows that any corresponding mass action system is complex balanced, and therefore exhibits 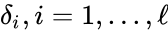 , denote the deficiencies of the individual linkage classes considered as their own networks. Suppose the following conditions:
, denote the deficiencies of the individual linkage classes considered as their own networks. Suppose the following conditions: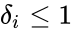 for all
for all 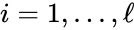 ,
,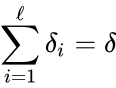 , and
, and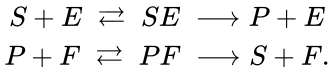
 stoichiometrically distinct
stoichiometrically distinct 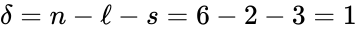 . The deficiency one theorem may not be applied, however, because the deficiency of each linkage class is
. The deficiency one theorem may not be applied, however, because the deficiency of each linkage class is 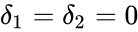 , so that
, so that 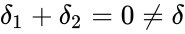 .
.
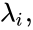
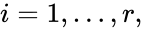 such that
such that  ,
,