Complex balanced mass action systems
A complex balanced equilibrium concentration of a mass action system is a point which satisfies
for . Using the short-hand notation we can rewrite this as for . A mass action system is said to be complex balanced if every equilibrium concentration permitted by the system is a complex balanced equilibrium concentration.
The notion of complex balancing of equilibrium concentrations was introduced in 1972 by Fritz Horn and Roy Jackson as a generalization of detailed balancing[1]. Is is a weaker than detailed balancing in that it does not require each elementary step in the reaction to be balanced by a reverse step, rather it requires that the net input into each complex balances the net flow out of the complex.
Matrix formulation
A complex balanced equilibrium concentration may be alternatively characterized by
where is the mass action vector, is the kinetic or Kirchhoff matrix, and is the -dimensional vector with all entries zero.
Properties of complex balanced mass action systems
A number of strong dynamical properties are known to hold for mass action systems with complex balanced equilibrium concentrations. Fritz Horn and Roy Jackson proved the follow results[1]:
- any mass action system permitting a complex balanced equilibrium concentration only permits complex balanced equilibrium concentrations (Lemma 5B);
- each stoichiometric compatibility class of a complex balanced system has exactly one equilibrium concentration (Theorem 6A and Lemma 4B); and
- that equilibrium concentration is locally asymptotically stable relative to its compatibility class (Theorem 6A and Lemma 4C).
The argument is made by use of the pseudo-Helmholtz function
where is any complex balanced equilibrium concentration permitted by the system. They were able to show that the time-derivative of the along solutions of a complex balanced mass action system satisfy
for all . This result is sufficient to prove trajectories are bounded, non-periodic and non-chaotic, and converge to the stoichiometrically compatible equilibrium concentration within a neighbourhood. It is unable, however, to preclude the possibility of trajectories approaching the boundary because is not radially unbounded relative to .
Fritz Horn was also able to show that complex balanced mass action systems share many connections with the reaction graph of the underlying chemical reaction network[2]. He was able to show that every chemical reaction network which permits a complex balanced mass action system is weakly reversible (Theorem 2B), that every chemical reaction network which is weakly reversible permits complex balanced mass action systems (discussion after Theorem 3B), and that a mass action system is unconditionally complex balanced (complex balanced for choices of its positive rate constants) if and only if it is weakly reversible and deficiency zero (Theorem 3B).
Global Attractor Conjecture
The Global Attractor Conjecture is the conjecture that the unique equilibrium concentration known to exist in each positive stoichiometric compatibility class of a complex balanced mass action system is a global attractor of the compatibility class. That is to say, every trajectory originating in converges asymptotically toward a unique point in the compatibility class (the stoichiometrically compatible complex balanced equilibrium concentration).
The belief that complex balanced mass action systems satisfy the conjecture has been widespread through chemical reaction network theory since complex balanced systems were introduced by Fritz Horn and Roy Jackson in 1972 [1]. The conjecture that the convergence to complex balanced equilibria extends globally to was first made by Fritz Horn in 1974 [3]. The problem has received significant attention since. It is known that in order to prove the conjecture, it is sufficient to prove that trajectories are persistent [4][5]. Consequently, there is a significant overlap between questions of persistence and attempts to prove the conjecture.
The conjecture was retitled the Global Attractor Conjecture in 2009 by Gheorghe Craciun, Alicia Dickenstein, Anne Shiu and Bernd Sturmfels [6]. The conjecture is currently one of the best known and widely studied problems in chemical reaction network theory [7].
References
- ↑ 1.0 1.1 1.2 Fritz Horn and Roy Jackson, General mass action kinetics, Arch. Ration. Mech. Anal., 47:81--116, 1972
- ↑ Fritz Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal., 49:172--186, 1972
- ↑ Fritz Horn, The dynamics of open reaction systems: mathematical aspects of chemical and biochemical problems and quantum chemistry, SIAM-AMS Proceedings, Vol. VIII, 125--137, 1974
- ↑ David Siegel and Debra MacLean, Global stability of complex balanced mechanisms, J. Math. Chem., 27(1-2):89--110, 2000
- ↑ Eduardo Sontag, Structure and stability of certain chemical networks and applications to the kinetic proofreading model of t-cell receptor signal transduction, IEEE Trans. Automat. Control, 46(7):1028--1047, 2001
- ↑ Gheorghe Craciun, Alicia Dickenstein, Anne Shiu, and Bernd Sturmfels, Toric dynamical systems, J. Symbolic Comput., 44(11):1551--1565, 2009
- ↑ David Anderson, A proof of the global attractor conjecture in the single linkage class case, SIAM J. Appl. Math., 71(4):1487--1508, 2011
![{\displaystyle {\vec {a}}=[a_{1},a_{2},\ldots ,a_{n}]^{T}\in \mathbb {R} _{>0}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/png/15acae80a6a527776a408e6582ece7bffcd07c78) is a point which satisfies
is a point which satisfies
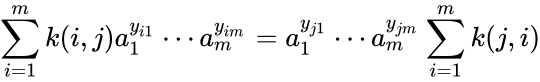
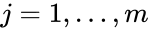 . Using the short-hand notation
. Using the short-hand notation 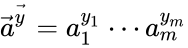 we can rewrite this as
we can rewrite this as 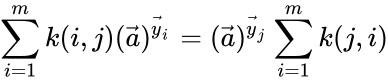 for
for 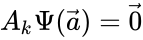
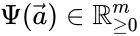 is the
is the  is the
is the 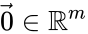 is the
is the 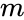 -dimensional vector with all entries zero.
-dimensional vector with all entries zero.
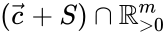 of a complex balanced system has exactly one equilibrium concentration (Theorem 6A and Lemma 4B); and
of a complex balanced system has exactly one equilibrium concentration (Theorem 6A and Lemma 4B); and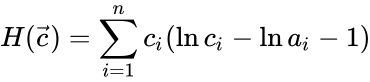
![{\displaystyle {\vec {a}}=[a_{1},\ldots ,a_{n}]^{T}\in \mathbb {R} _{>0}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/png/5990a24662da6e9e5bd76db642e27922fc30743a) is any complex balanced equilibrium concentration permitted by the system. They were able to show that the time-derivative of the
is any complex balanced equilibrium concentration permitted by the system. They were able to show that the time-derivative of the 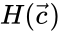 along solutions
along solutions 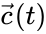 of a complex balanced mass action system satisfy
of a complex balanced mass action system satisfy
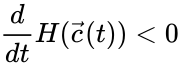
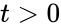 . This result is sufficient to prove trajectories are bounded, non-periodic and non-chaotic, and converge to the stoichiometrically compatible equilibrium concentration within a neighbourhood. It is unable, however, to preclude the possibility of trajectories approaching the boundary
. This result is sufficient to prove trajectories are bounded, non-periodic and non-chaotic, and converge to the stoichiometrically compatible equilibrium concentration within a neighbourhood. It is unable, however, to preclude the possibility of trajectories approaching the boundary ![{\displaystyle \partial [({\vec {c}}_{0}+S)\cap \mathbb {R} _{>0}^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/1c38e608cd94cf492cc132bd8530ce7614b4b199) because
because 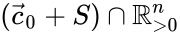 .
.
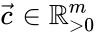 known to exist in each positive
known to exist in each positive  of a complex balanced mass action system is a global attractor of the compatibility class. That is to say, every trajectory originating in
of a complex balanced mass action system is a global attractor of the compatibility class. That is to say, every trajectory originating in 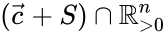 was first made by Fritz Horn in 1974
was first made by Fritz Horn in 1974