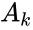Kinetic matrix
Consider a chemical reaction network endowed with mass-action kinetics and using complex-centered indexing of the reactions and rate constants , for . Then the kinetic or Kirchhoff matrix of the system is defined as
where is the rate constant corresponding to the reaction (and if ).
The kinetic matrix of a system keeps track of the connections in the reaction graph of a network, as well as the corresponding reaction weights associated with mass-action kinetics. For example, for off-diagonal entries , it is clear that for all and if and only if . In this sense, a kinetics matrix can be said to indicate the structure of a chemical reaction network underlying a mass action system. It is also clear that where and are the vectors of all ones and zeroes, respectively. This implies, among other things, that a kinetics matrix has a non-trivial kernel.
The kinetics matrix differs from the weighted Laplacian matrix of a weighted directed graph only by the sign of its entries.
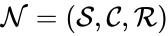 endowed with
endowed with 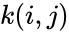 , for
, for 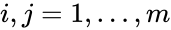 . Then the kinetic or Kirchhoff matrix
. Then the kinetic or Kirchhoff matrix 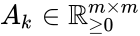 of the system is defined as
of the system is defined as
![{\displaystyle A_{k}=\left[{\begin{array}{cccc}-\sum _{i=1}^{m}k(1,i)&k(2,1)&\cdots &k(m,i)\\k(1,2)&-\sum _{i=1}^{m}k(2,i)&\cdots &k(m,2)\\\vdots &\vdots &\ddots &\vdots \\k(1,m)&k(2,m)&\cdots &-\sum _{i=1}^{m}k(m,i)\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/c2c964fba09dcbacfd9e2f4c793f979d4fd6e894)
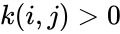 is the rate constant corresponding to the reaction
is the rate constant corresponding to the reaction  (and
(and 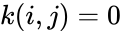 if
if 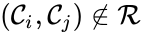 ).
).
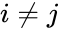 , it is clear that
, it is clear that ![{\displaystyle [A_{k}]_{ji}\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/png/e6cc62aadf76cb40f9034b2b2d8dfff9b1a6152f) for all
for all 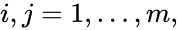 and
and ![{\displaystyle [A_{k}]_{ji}>0}](https://wikimedia.org/api/rest_v1/media/math/render/png/1d32a52915d2eaa062797f71345e7752db92383e) if and only if
if and only if 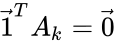 where
where 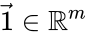 and
and 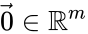 are the vectors of all ones and zeroes, respectively. This implies, among other things, that a kinetics matrix has a non-trivial kernel.
are the vectors of all ones and zeroes, respectively. This implies, among other things, that a kinetics matrix has a non-trivial kernel.