Generalized mass action systems
A generalized chemical reaction network is given by a chemical reaction network together with an additional set of kinetic complexes which are in one-to-one correspondence with the complex set . The basic idea is that the first complex set, , controls the stoichiometry of the network while the second complex set, , controls the kinetics. That is, the first dictates the reaction vectors while the second dictates the mass action monomials. A generalized chemical reaction network is denoted .
Generalized mass action systems
A generalized chemical reaction network can be corresponded with a mass action system in a similar way as a normal chemical reaction network. In particular, we assign kinetic rates and reaction stoichiometry according to the reaction graph. We, however, substitute the stoichiometry of the corresponding kinetic complexes when determining the mass action monomials. This leads to the generalized mass action system
where is the kinetic complex associated with . Generalized mass action systems may also be represented in the form
where and are as defined according to the network , and is defined with respect to the network .
Because generalized chemical reaction networks have twice as many complexes as a standard chemical reaction network, it is often difficult to represent them graphically. When space is not a concern, the kinetic complex may be indicated in the reaction graph by a dotted line. For example, we may write
to indicate that the complex is associated with the kinetic complex , and the complex is associated with the kinetic complex . In general, it may be necessary to include only the stoichiometric complexes in the graphical representation and to indicate the correspondence with kinetic complexes in a supplemental table.
In the above example, if we allow the forward reaction to have reaction rate and the backward reaction to have rate , the generalized mass action system is given by
Kinetic reaction graph
In addition to , to each generalized chemical reaction network we may associated a kinetic-order reaction graph . We define the kinetic-order subspace
and the kinetic-order deficiency where . That is to say, we determine the properties for in exactly the same way as we do for a standard reaction graph. It is important to recognize, however, that the quantities are applied differently in the analysis of generalized mass action systems than for standard ones.
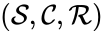 together with an additional set of kinetic complexes
together with an additional set of kinetic complexes 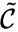 which are in one-to-one correspondence with the complex set
which are in one-to-one correspondence with the complex set  . The basic idea is that the first complex set,
. The basic idea is that the first complex set, 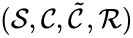 .
.
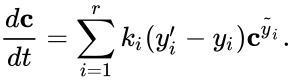
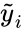 is the kinetic complex associated with
is the kinetic complex associated with 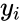 . Generalized mass action systems may also be represented in the form
. Generalized mass action systems may also be represented in the form
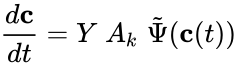
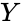 and
and 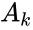 are as defined according to the network
are as defined according to the network 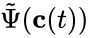 is defined with respect to the network
is defined with respect to the network 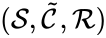 .
.
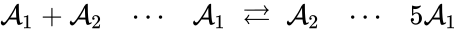
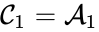 is associated with the kinetic complex
is associated with the kinetic complex 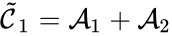 , and the complex
, and the complex 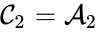 is associated with the kinetic complex
is associated with the kinetic complex 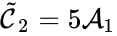 . In general, it may be necessary to include only the stoichiometric complexes in the graphical representation and to indicate the correspondence with kinetic complexes in a supplemental table.
. In general, it may be necessary to include only the stoichiometric complexes in the graphical representation and to indicate the correspondence with kinetic complexes in a supplemental table.
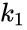 and the backward reaction to have rate
and the backward reaction to have rate 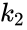 , the generalized mass action system is given by
, the generalized mass action system is given by
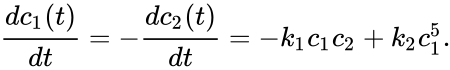
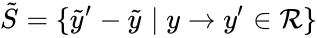
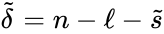 where
where 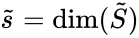 . That is to say, we determine the properties for
. That is to say, we determine the properties for