CoNtRol
This page documents the CoNtRol web interface. It is currently very much a work in progress.
Introduction
CoNtRol (CRN tool) is a web application that allows users to run various tests to determine the possible dynamics of chemical reaction networks. It is intended to be an open framework allowing researchers to build on each other's work by adding new tests as new developments occur. The reference implementation is available at http://reaction-networks.net/control/.
User Documentation
There are a number of ways to use CoNtRol. The most basic way is to type a set of reactions into the web page and view the results of the analysis online. This mode also offers a number of helper functions, such as a Java Web Start application to draw the DSR graph and a function to generate LaTeX describing the reactions. Users can also save the chemical reaction network structure in a text file for future analysis. It is also possible to upload a set of chemical reactions in a variety of file formats.
More advanced users can edit options to disable some of the tests, or to restrict tests to mass action kinetics (for tests that support this restriction). For users with multiple reaction networks to analyse, there is also a feature to upload a batch of networks for analysis, with the results being sent to the user via email.
The individual tools that make up CoNtRol can also be built and run individually on users’ local machines if preferred. The web interface is purely intended to help simplify the use of multiple tools.
Pre-built versions of CoNtRol are available for download at http://reaction-networks.net/control/download/.
TO DO: include documentation about running individual components manually. Link to individual component downloads once they are available.
Basic Usage
The simplest way to use CoNtRol is simply to type a set of reactions into the main input form. Pressing the “Analyse CRN” button will then begin analysis of the CRN and load the results once the calculations are complete. By default, all tests are run, and debugging output is not included. At the bottom of the results are buttons to generate the DSR graph of the CRN, and to email the calculated results for later use.
To remove all reactions and reset any stored results, click the “--” button.
Advanced Usage
CoNtRol offers several advanced options:
- Download/upload of a file describing a CRN (to simplify the re-analysis of a CRN, or to allow input of a CRN from a catalogue of CRNs)
- Upload of a zip archive containing multiple CRN descriptor files
- Enable/disable certain tests
- Turn on/off extra debugging output
- Automatic generation of LaTex markup describing the CRN chemical equations and stoichiometry matrix, and TikZ markup describing the DSR graph
By default, the Analysis menu only shows the “Analyse CRN” and “Options” buttons. The “Options” button allows users to enable/disable tests and debugging (detailed test output) mode. Clicking “More” at the bottom of the Analysis menu offers the ability to download a CRN descriptor file, to generate LaTeX for the reaction equations and stoichiometry matrix, and to launch the DSR graph application.
The File Input menu is hidden by default. Clicking “Show” allows the user to upload either a single file, for analysis within the web page, or a batch file for delayed analysis. In both modes, currently supported CRN file formats are listed. Batch files must consist of a zip archive containing one or more text files representing CRNs, all in the same format.
DSR graph application
CoNtRol includes a Java Web Start application to draw the DSR graph. It can be launched from the Analysis menu, or from the button at the bottom of the results page. The reaction and reactant nodes can be moved around with the mouse. Clicking the “Export to LaTeX” button will open a dialogue to save a file containing TikZ markup describing the DSR graph.
Note: when using Google Chrome/Chromium with default settings, the DSR graph will not launch automatically in Java Web Start. See https://code.google.com/p/chromium/issues/detail?id=10877#c206 for a workaround for this issue.
Running the DSR graph application requires that Java be installed on the user’s computer. Unfortunately this means that the DSR graph feature cannot be used on mobile devices. All other CoNtRol features should work on mobile devices, including Android and iOS smartphones and tablets.
Developer Documentation
The entire CoNtRol application is open source, to promote its re-use and development by as wide a number of researchers as possible. Developers can browse the entire source tree at http://reaction-networks.net/control/download/source. Currently the web application is only supported on Linux servers, although we believe that it will also run on Mac OS X with some custom PHP modules. There are no plans for Windows support at the moment but we believe that it should run under Cygwin (feedback/testing results appreciated). Windows users can still use CoNtRol via a browser, it is only not supported for Windows servers. Additionally, some/all of the individual components should run on Windows.
CoNtRol currently consists of five components, written in different languages. The user interface and server “glue” that launches the tests and fetches results is written in PHP, with the display component written in standards compliant XHTML 1.1/CSS/jQuery/JavaScript. The DSR graph display is a Java Web Start application. The “General analysis“ (analysereacs) test is written in C. The “DSR” (dsrtest) test is written in GNU Octave. The “Jacobian” (calc-jacobian) test is written in Maxima, with some PHP and POSIX shell script wrapper code around it.
New tests can be implemented as plugins in (theoretically) any language, including scripts for proprietary tools such as MATLAB, Mathematica, etc, although they may require some shell scripting glue to fit into the CoNtRol architecture.
Plugin Architecture
New plugins can be added by providing the following:
- An executable file that can be invoked via the command line using the form
plugin [--mass-action-only] filename- The
--mass-action-onlyflag is optional, and is only required for executables that support both mass action and general kinetics. - The executable can either be a compiled binary, or a shell script, which may in turn simply be a wrapper calling other binaries or scripts.
- The
- An array describing the plugin, to be added to
includes/standard-tests.php. Examples are provided.
File Formats
CoNtRol currently supports four file formats, although there is scope to add more in the future if there is a requirement for them. All currently supported file formats are plain text. Samples of each are shown below for the reaction network
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \rightarrow B + C \rightleftharpoons 2B}
Net Stoichiometry
-1 0 0 1 1 -1 1 -1 1
This format is very simple but also very limited, as it does not show whether each reaction is reversible or irreversible, nor does it show if a reactant appears on both sides of a reaction. Currently CoNtRol assumes that all reactions are irreversible and that no reactant appears on both sides of a reaction when this file format is used. To represent a reversible reaction, it is necessary to include both the forwards and backwards reactions.
Net Stoichiometry + V Matrix
S MATRIX -1 0 1 1 1 -1 V MATRIX 1 0 0 2 0 1
This format is slightly less limited as it can distinguish reversible and irreversible reactions. The zeros in the first column of the V matrix show that the reaction is irreversible. By convention, a 2 in the V matrix represents ±, i.e. the reaction rate can depend positively or negatively on the reactant concentration at different points in phase space.
Source Stoichiometry + Target Stoichiometry
S MATRIX 1 0 0 0 1 2 0 1 0 T MATRIX 0 0 0 1 2 1 1 0 1
Source Stoichiometry + Target Stoichiometry + V Matrix
S MATRIX 1 0 0 1 0 1 T MATRIX 0 0 1 2 1 0 V MATRIX 1 0 0 2 0 1 REVERSIBLE 0 1
This format includes all information about the reactions.
Human Readable
A --> B + C B + C <--> 2B
This format includes all information about the reactions. Note that the two reactions are represented on separate lines, despite both having the complex Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B + C} in common.
TO DO: Finalise modulators in file formats and describe them here.
Terminology and notation
Nonnegative vector, positive vector
An vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \in \mathbb{R}^n} is termed nonnegative (and we write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \geq 0} ) if each of its components is nonnegative, i.e., Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \in \mathbb{R}^n_{\geq 0}} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is termed positive (and we write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \gg 0} ) if each of its components is positive, i.e., Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \in \mathrm{int}\,\mathbb{R}^n_{\geq 0}} .
Stoichiometric subspace and stoichiometry classes
The stoichiometric subspace of a CRN is the image of the stoichiometric matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma} . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma \in \mathbb{R}^{n \times m},} the stoichiometric subspace is a linear subspace of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{n}} .
Stoichiometry classes, also known as a “stoichiometric compatibility classes” of a CRN with stoichiometric matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma} are the sets formed by intersection of cosets of the stoichiometric subspace with the nonnegative orthant. I.e. given Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma \in \mathbb{R}^{n \times m},} the stoichiometry class of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \in \mathbb{R}^n_{\geq 0}} is the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (y + \mathrm{im}\,\Gamma) \cap \mathbb{R}^n_{\geq 0}} . Given a system of the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \mathbb{R}^n} and such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} is forward invariant, the stoichiometry classes are clearly forward invariant sets for the system. A stoichiometry class is termed “nontrivial” if it includes a positive vector (i.e., it intersects Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{int}\,\mathbb{R}^n_{\geq 0}} ).
Stoichiometry classes are bounded if and only if kerFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\Gamma^t} includes a positive vector; equivalently if and only if imFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\Gamma} includes a nonnegative and nonzero vector. A bounded, nonempty stoichiometry class is an invariant compact polyhedron, and so must include an equilibrium by the Brouwer fixed-point theorem.
Compatible vectors/equilibria
Given a system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} , two vectors are “compatible” if they belong to the same stoichiometry class. In particular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x,y} are compatible equilibria if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x, y \in \mathbb{R}^n_{\geq 0}} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(x) = \Gamma v(y) = 0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y - x \in \mathrm{im}\,\Gamma} .
Reaction system with arbitrary inflows and outflows
Also known as a “fully open system”. Consider a reaction system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in \mathbb{R}^n} . Then given any nonnegative vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{in}} and any Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C^1} function with derivative Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DQ} which is positive and diagonal on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} , the new system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = C_{in} + \Gamma v(x) - Q(x)} will be termed “the system with arbitrary inflows and outflows”. If a claim is made for “the system with arbitrary inflows and outflows”, this means that the claim must hold true for all nonnegative vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{in}} and functions Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} satisfying the assumptions above.
Siphon
A siphon of a CRN is a set of chemical species Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} such that if the concentrations of each species of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is zero, then no reaction is able to produce any species of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} (for general kinetics). In other words if the concentrations of species in a siphon are set to zero, then they remain zero for all time. Given an ordered set of substrates, we can regard as siphon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} as a nonempty, proper, subset of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{1, \ldots n\}} . Corresponding to such an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \subseteq \{1, \ldots, n\}} is a face of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x \in \mathbb{R}^n_{\geq 0}\colon x_i = 0\,\,\mbox{if}\,\, i \in S\}} . It is easy to see that if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is a siphon, then is invariant under weak assumptions on the reaction kinetics.
MPNE
“Multiple positive nondegenerate equilibria”: when there are two or more positive equilibria on a stoichiometry class and the reduced Jacobian determinant is nonzero at each of these equilibria.
Persistence-type conditions
Persistence condition 1 (PC1)
The boundary of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} includes no equilibria other than the origin. This can be claimed for general kinetics if, for example, the system has no siphons.
Persistence condition 2 (PC2)
No nontrivial stoichiometry class includes any equilibria on the boundary of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} . This can be claimed for general kinetics if, for example, no nontrivial stoichiometry class intersects a face of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} corresponding to a siphon. A CRN satisfying PC2 can be termed structurally persistent.
Persistence condition 3 (PC3)
No initial condition in has omega limit set intersecting the boundary of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} . (This is persistence in the usual sense.) This may occur for mass action kinetics even when some nontrivial stoichiometry class intersects a face of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} corresponding to a siphon. The persistence conjecture states that all weakly reversible CRNs with mass action kinetics are persistent.
Injectivity-type conditions
Injectivity condition 1 (IC1)
The system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} satisfies condition IC1 if: and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y - x \in \mathrm{im}\,\Gamma\backslash\{0\}]} implies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)} . In other words, the vector field cannot take the same value at two distinct compatible vectors both in the interior of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} . This can be phrased briefly as “the system forbids multiple compatible positive equilibria”.
Injectivity condition 1a (IC1a)
The system satisfies condition IC1a if: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x,y \in \mathbb{R}^n_{\geq 0}, y - x \in \mathrm{im}\,\Gamma\backslash\{0\}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x)+v(y) \gg 0} ], imply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)} .
Injectivity condition 1'' (IC1'')
The system satisfies condition IC1'' if: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x,y \in \mathbb{R}^n_{\geq 0}} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y - x \in \mathrm{im}\,\Gamma\backslash\{0\}} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) = \Gamma v(x)]} together imply that and in fact both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} belong to the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} . In other words, if the vector field takes the same value at two distinct compatible vectors, then they must both be on the boundary of and in fact on the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} .
In particular, the practically important conclusions are: (i) any positive equilibrium is the unique equilibrium on its stoichiometry class; (ii) if a stoichiometry class includes a boundary equilibrium Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} , then all equilibria on the stoichiometry class of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} must belong to a single facet of .
Injectivity condition 2 (IC2)
The system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} satisfies condition IC2 if the associated system with arbitrary inflows and outflows Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = C_{in} + \Gamma v(x) - Q(x)} is injective on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\gg 0}} . In particular it has at most one equilibrium in . A corollary is that the original system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} cannot have MPNE.
Injectivity condition 2'' (IC2'')
The system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)} satisfies condition IC2'' if the associated system with arbitrary inflows and outflows Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = C_{in} + \Gamma v(x) - Q(x)} is injective on . In particular it has at most one equilibrium in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}} .
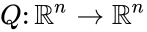 with derivative Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DQ}
which is positive and diagonal on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
, the new system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = C_{in} + \Gamma v(x) - Q(x)}
will be termed “the system with arbitrary inflows and outflows”. If a claim is made for “the system with arbitrary inflows and outflows”, this means that the claim must hold true for all nonnegative vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{in}}
and functions Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q}
satisfying the assumptions above.
with derivative Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle DQ}
which is positive and diagonal on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
, the new system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = C_{in} + \Gamma v(x) - Q(x)}
will be termed “the system with arbitrary inflows and outflows”. If a claim is made for “the system with arbitrary inflows and outflows”, this means that the claim must hold true for all nonnegative vectors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{in}}
and functions Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q}
satisfying the assumptions above.
 substrates, we can regard as siphon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
as a nonempty, proper, subset of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{1, \ldots n\}}
. Corresponding to such an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \subseteq \{1, \ldots, n\}}
is a face
substrates, we can regard as siphon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
as a nonempty, proper, subset of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{1, \ldots n\}}
. Corresponding to such an Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \subseteq \{1, \ldots, n\}}
is a face 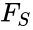 of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x \in \mathbb{R}^n_{\geq 0}\colon x_i = 0\,\,\mbox{if}\,\, i \in S\}}
. It is easy to see that if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
is a siphon, then
of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x \in \mathbb{R}^n_{\geq 0}\colon x_i = 0\,\,\mbox{if}\,\, i \in S\}}
. It is easy to see that if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
is a siphon, then 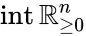 has omega limit set intersecting the boundary of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. (This is persistence in the usual sense.) This may occur for mass action kinetics even when some
has omega limit set intersecting the boundary of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. (This is persistence in the usual sense.) This may occur for mass action kinetics even when some 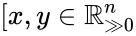 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y - x \in \mathrm{im}\,\Gamma\backslash\{0\}]}
implies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)}
. In other words, the vector field cannot take the same value at two distinct compatible vectors both in the interior of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. This can be phrased briefly as “the system forbids multiple compatible positive equilibria”.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y - x \in \mathrm{im}\,\Gamma\backslash\{0\}]}
implies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)}
. In other words, the vector field cannot take the same value at two distinct compatible vectors both in the interior of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. This can be phrased briefly as “the system forbids multiple compatible positive equilibria”.
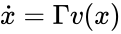 satisfies condition IC1a if: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x,y \in \mathbb{R}^n_{\geq 0}, y - x \in \mathrm{im}\,\Gamma\backslash\{0\}}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x)+v(y) \gg 0}
], imply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)}
.
satisfies condition IC1a if: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x,y \in \mathbb{R}^n_{\geq 0}, y - x \in \mathrm{im}\,\Gamma\backslash\{0\}}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(x)+v(y) \gg 0}
], imply Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma v(y) \neq \Gamma v(x)}
.
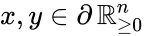 and in fact both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
belong to the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. In other words, if the vector field takes the same value at two distinct compatible vectors, then they must both be on the boundary of
and in fact both Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
belong to the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
. In other words, if the vector field takes the same value at two distinct compatible vectors, then they must both be on the boundary of 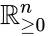 and in fact on the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
.
and in fact on the same facet of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n_{\geq 0}}
.
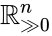 . A corollary is that the original system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)}
cannot have
. A corollary is that the original system Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x = \Gamma v(x)}
cannot have